Advertisements
Advertisements
Question
The angle of elevation of the top of a tower as observed form a point in a horizontal plane through the foot of the tower is 32°. When the observer moves towards the tower a distance of 100 m, he finds the angle of elevation of the top to be 63°. Find the height of the tower and the distance of the first position from the tower. [Take tan 32° = 0.6248 and tan 63° = 1.9626]
Solution
Let h be the height of the tower and the angle of elevation as observed from the foot of the tower is 32° and observed move towards the tower with distance 100 m then the angle of elevation becomes 63°.
Let BC = x and CD = 100
Now we have to find the height of the tower
So we use trigonometrical ratios.
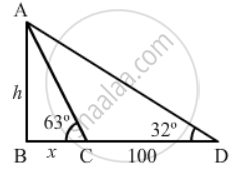
In a triangle ABC,
`=> tan C = (AB)/(BC)`
`=> tan 63^@ = (AB)/(BC)`
`=> 1.9626 = h/x`
`=> x = h/1.9626`
Again in a triangle ABD
`=> tan D = (AB)/(BC + CD)`
`=> tan 32^@ = h/(x + 100)`
`=> 0.6248 = h/(x + 100)`
`=> x + 100 = h/0.6248`
`=> 100 = h/0.6248 - h/1.9626`
`=> 100 = (h xx 1.9626 - h xx 0.6248)/(0.6248 xx 1.9626)`
`=> 100 = (h(1.9626 - 0.6248))/(0.6248 xx 1.9626)`
`=> 100 = (h(1.3378))/(0.6248 xx 1.9626)`
=> 100 x 0.6248 x 1.9626 = h x 1.3378
`=> h = (100 xx 0.6248 xx 1.9626)/1.3378`
`=> 122.6232/1.3378`
=> 91.66
`=> x = 91.66/1.9626`
= 46.7
So distance of the first position from the tower is = 100 + 46.7 = 146.7 m
Hence the height of tower 91.66 m and the desires distance is 146.7 m
APPEARS IN
RELATED QUESTIONS
The angle of depression of a car parked on the road from the top of a 150 m high tower is 30°. The distance of the car from the tower (in metres) is
`(A) 50sqrt3`
`(B) 150sqrt 3`
`(C) 150sqrt2`
`(D) 75`
On a straight line passing through the foot of a tower, two points C and D are at distances of 4 m and 16 m from the foot respectively. If the angles of elevation from C and D of the top of the tower are complementary, then find the height of the tower.
The angle of elevation of a stationary cloud from a point 2500 m above a lake is 15° and the angle of depression of its reflection in the lake is 45°. What is the height of the cloud above the lake level? (Use tan 15° = 0.268)
The horizontal distance between two towers is 60 meters. The angle of depression of the top of the first tower when seen from the top of the second tower is 30° . If the height of the second tower is 90 meters. Find the height of the first tower.
The angle of depression form the top of a tower of a point A on the ground is 30° . On moving a distance of 20 meters from the point A towards the foot of the tower to a point B, the angle of elevation of the top of the tower to from the point B is 60° . Find the height of the tower and its distance from the point A.
A bucket is in the form of a frustum of a cone and it can hold 28.49 litres of water. If the radii of its circular ends are 28 cm and 21 cm, find the height of the bucket. [Use`pi22/7` ]
The height of a tower is 10 m. What is the length of its shadow when Sun's altitude is 45°?
Find the positive value of m for which the distance between the points A(5, −3) and B(13, m) is 10 units.
A road is flanked on either side by continuous rows of houses of height `4sqrt(3)` m with no space in between them. A pedestrian is standing on the median of the road facing a row house. The angle of elevation from the pedestrian to the top of the house is 30°. Find the width of the road
The angle of elevation of the top of a 15 m high tower at a point `15sqrt(3)` m away from the base of the tower is ______.
