Advertisements
Advertisements
Question
Find the positive value of m for which the distance between the points A(5, −3) and B(13, m) is 10 units.
Solution
It is given that distance between A(5, −3) and B(13, m) is 10 units.
⇒ `"AB" = sqrt((5-13)^2 +(-3-"m")^2)`
⇒ `10 = sqrt(64+9+6"m"+"m"^2)`
⇒ 100 = 73 + 6m +m2
⇒ m2 + 6m - 27 = 0
⇒ m2 +9m - 3m - 27 =0
⇒ m (m+9) - 3 (m-9)=0
⇒ (m-3) (m+9) =0
⇒ m=3, -9
Hence, the positive value of m is 3.
APPEARS IN
RELATED QUESTIONS
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff. At a point on the plane 70 metres away from the tower, an observer notices that the angles of elevation of the top and the bottom of the flagstaff are respectively 60° and 45°. Find the height of the flag-staff and that of the tower.
The shadow of a tower standing on a level ground is found to be 40 m longer when Sun’s altitude is 30° than when it was 60°. Find the height of the tower.
A tree standing on a horizontal plane is leaning towards the east. At two points situated at distances a and b exactly due west on it, the angles of elevation of the top are respectively α and β. Prove that the height of the top from the ground is `((b - a)tan alpha tan beta)/(tan alpha - tan beta)`
On a horizonal plane there is a vertical tower with a flagpole on the top of the tower. At a point, 9 meters away from the foot of the tower, the angle of elevation of the top and bottom of the flagpole are 60 and 30 respectively. Find the height of the tower and the flagpole mounted on it.
Two poles of equal heights are standing opposite to each other on either side of the road which is 80m wide, From a point P between them on the road, the angle of elevation of the top of one pole is 60 and the angle of depression from the top of another pole at P is 30 . Find the height of each pole and distance of the point P from the poles.
The angle of depression form the top of a tower of a point A on the ground is 30° . On moving a distance of 20 meters from the point A towards the foot of the tower to a point B, the angle of elevation of the top of the tower to from the point B is 60° . Find the height of the tower and its distance from the point A.
From a light house the angles of depression of two ships on opposite sides of the light house are observed to be 30° and 45°. If the height of the light house is h metres, the distance between the ships is
A statue 1.6 m tall stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60ϒ and from the same point the angle of elevation of the top of the pedestal is 40ϒ. Find the height of the pedestal. (tan 40° = 0.8391, `sqrt(3)` = 1.732)
The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Then the height of the tower is ____________.
|
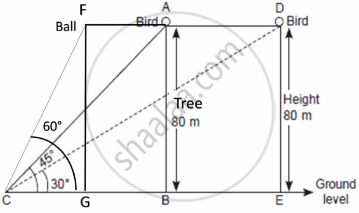
One evening, Kaushik was in a park. Children were playing cricket. Birds were singing on a nearby tree of height 80m. He observed a bird on the tree at an angle of elevation of 45°. When a sixer was hit, a ball flew through the tree frightening the bird to fly away. In 2 seconds, he observed the bird flying at the same height at an angle of elevation of 30° and the ball flying towards him at the same height at an angle of elevation of 60°.
|
- At what distance from the foot of the tree was he observing the bird sitting on the tree?
- How far did the bird fly in the mentioned time?
(or)
After hitting the tree, how far did the ball travel in the sky when Kaushik saw the ball? - What is the speed of the bird in m/min if it had flown `20(sqrt3 + 1) m`?