Advertisements
Advertisements
प्रश्न
A vertically straight tree, 15 m high, is broken by the wind in such a way that its top just touches the ground and makes an angle of 60° with the ground. At what height from the ground did the tree break?
उत्तर
Let AB be the tree of desired height x m and tree is broken by wind then tree makes an angle C = 60°. Let AC = 15 - x
Here we have to find height x
So we use trigonometric ratios.
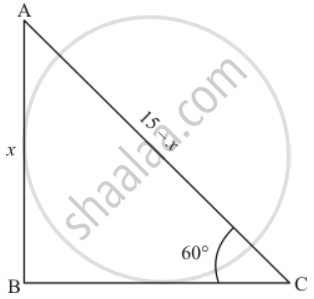
In a triangle ACB
=> `sin C = (AB)/(AC)`
`=> sin 60^@ = x/(15 - x)`
`=> sqrt3/2 = x/(15 - x)`
`=> 15sqrt3 - sqrt3x = 2x`
`=> 15sqrt3 = 2x + sqrt3x`
`=> 15sqrt3 = x(2 + sqrt3)`
`=> x = (15sqrt3)/(2 +sqrt3)`
=> x = 6.9
Hence the height of tree is 6.9 m
APPEARS IN
संबंधित प्रश्न
A bus travels at a certain average speed for a distance of 75 km and then travels a distance of 90 km at an average speed of 10 km/h more than the first speed. If it takes 3 hours to complete the total journey, find its first speed?
The altitude of the sun at any instant is 60º. Find the height of the vertical pole that will cast a shadow of 30 m.
When the sun is 30º above the horizontal, Find the length of shadow cast by a building 50m high
A ladder rests against a wall at an angle α to the horizontal. Its foot is pulled away from the wall through a distance a so that it slides a distance b down the wall making an angle β with the horizontal. Show that `a/b = (cos alpha - cos beta)/(sin beta - sin alpha)`
From a point on the ground, 20 m away from the foot of a vertical tower, the angle elevation of the top of the tower is 60°, What is the height of the tower?
The height of the vertical pole is \[\sqrt{3}\] times the length of its shadow on the ground, then angle of elevation of the sun at that time is
When an observer at a distance of 12 m from a tree looks at the top of the tree, the angle of elevation is 60°. What is the height of the tree? `(sqrt 3 = 1.73)`
Two towers A and B are standing some distance apart. From the top of tower A, the angle of depression of the foot of tower B is found to be 30°. From the top of tower B, the angle of depression of the foot of tower A is found to be 60°. If the height of tower B is ‘h’ m then the height of tower A in terms of ‘h’ is ____________ m.
A window of a house is h meters above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be A and B respectively. Then the height of the other house is ____________.
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 30°. Determine the height of the tower.
