Advertisements
Advertisements
Question
A vertically straight tree, 15 m high, is broken by the wind in such a way that its top just touches the ground and makes an angle of 60° with the ground. At what height from the ground did the tree break?
Solution
Let AB be the tree of desired height x m and tree is broken by wind then tree makes an angle C = 60°. Let AC = 15 - x
Here we have to find height x
So we use trigonometric ratios.
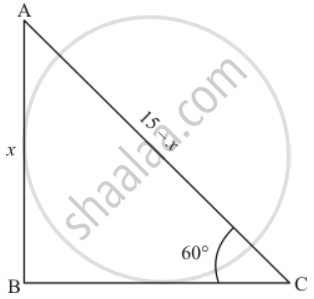
In a triangle ACB
=> `sin C = (AB)/(AC)`
`=> sin 60^@ = x/(15 - x)`
`=> sqrt3/2 = x/(15 - x)`
`=> 15sqrt3 - sqrt3x = 2x`
`=> 15sqrt3 = 2x + sqrt3x`
`=> 15sqrt3 = x(2 + sqrt3)`
`=> x = (15sqrt3)/(2 +sqrt3)`
=> x = 6.9
Hence the height of tree is 6.9 m
APPEARS IN
RELATED QUESTIONS
Two ships are there in the sea on either side of a light house in such a way that the ships and the light house are in the same straight line. The angles of depression of two ships as observed from the top of the light house are 60° and 45°. If the height of the light house is 200 m, find the distance between the two ships. [use √3=1.73]
The angle of elevation of the top of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40 m vertically above X, the angle of elevation of the top is 45°. Calculate the height of the tower.
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestones on opposite sides of the aeroplane are observed to be α and β. Show that the height in miles of the aeroplane above the road is given by `(tan alpha tan beta)/(tan alpha + tan beta)`
From the top of a light house, the angles of depression of two ships on the opposite sides of it are observed to be α and β. If the height of the light house be h metres and the line joining the ships passes through the foot of the light house, show that the distance between the ship is
`(h (tan ∝+tan ß))/ (tan ∝+tan ∝)`
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with horizontal, then the length of the wire is
On a morning walk, three persons step out together and their steps measure 30 cm, 36 cm, and 40 cm respectively. What is the minimum distance each should walk so that each can cover the same distance in complete steps?
From the top of a lighthouse, the angle of depression of two ships on the opposite sides of it is observed to be 30° and 60°. If the height of the lighthouse is h meters and the line joining the ships passes through the foot of the lighthouse, show that the distance between the ships is `(4"h")/sqrt(3)` m
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is C to the East of B?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
A TV tower stands vertically on a bank of a canal, with a height of `10 sqrt3` m. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the distance between the opposite bank of the canal and the point with a 30° angle of elevation.
The angles of elevation of the top of a tower from two points distant s and t from its foot are complementary. Then the height of the tower is ____________.
