Advertisements
Advertisements
प्रश्न
The height of the vertical pole is \[\sqrt{3}\] times the length of its shadow on the ground, then angle of elevation of the sun at that time is
विकल्प
30º
60º
45º
75º
उत्तर
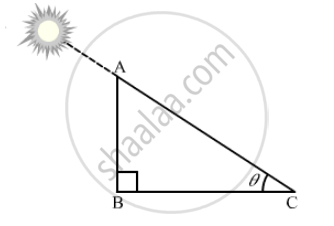
Let the angle of elevation of the sun be θ.
Suppose AB is the height of the pole and BC is the length of its shadow.
It is given that, AB = \[\sqrt{3}\]BC
In right ∆ABC,
\[\tan\theta = \frac{AB}{BC}\]
\[ \Rightarrow \tan\theta = \frac{\sqrt{3}BC}{BC} = \sqrt{3}\]
\[ \Rightarrow \tan\theta = \tan60°\]
\[ \Rightarrow \theta = 60°\]
Thus, the angle of elevation of the sun is 60º.
APPEARS IN
संबंधित प्रश्न
The heights of two poles are 80 m and 62.5 m. If the line joining their tops makes an angle of 45º with the horizontal, then find the distance between the pole
A man observes a car from the top of a tower, which is moving towards the tower with a uniform speed. If the angle of depression of the car changes from 30° to 45° in 12 minutes, find the time taken by the car now to reach the tower.
As observed from the top of a 100 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships. [Use `sqrt3` = 1.732]
A boy is standing on the ground and flying a kite with 100 m of string at an elevation of 30°. Another boy is sanding on the roof of a 10 m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
The angle of elevation of the top of a vertical tower from a point on the ground is 60° . From another point 10 m vertically above the first, its angle of elevation is 30° .Find the height of the tower.
A man on the deck of a ship, 16m above water level, observe that that angle of elevation and depression respectively of the top and bottom of a cliff are 60° and 30° . Calculate the distance of the cliff from the ship and height of the cliff.
In fig. 9 is shown a right circular cone of height 30 cm. A small cone is cut off from the top by a plane parallel to the base. If the volume of the small cone is 127127 of the volume of cone, find at what height above the base is the section made.
A vessel full of water is in the form of an inverted cone of height 8 cm and the radius of its top, which is open, is 5 cm. 100 spherical lead balls are dropped into the vessel. One-fourth of the water flows out of the vessel. Find the radius of a spherical ball ?
If the ratio of the height of a tower and the length of its shadow is `sqrt3:1`, what is the angle of elevation of the Sun?
At a point on level ground, the angle of elevation of a vertical tower is, found to be α such that tan α = `1/3`. After walking 100 m towards the tower, the angle of elevation β becomes such that tan β = `3/4`. Find the height of the tower.
