Advertisements
Advertisements
प्रश्न
Two buildings are facing each other on a road of width 12 metre. From the top of the first building, which is 10 metre high, the angle of elevation of the top of the second is found to be 60°. What is the height of the second building ?
उत्तर
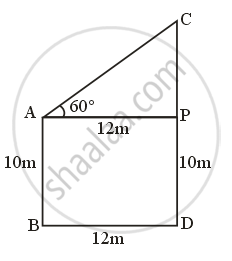
Let AB and CD be two building, with
AB = 10 m
And angle of elevation from top of AB to top of CD = ∠CAP = 60°
Width of road = BD = 12 m
Clearly, ABDP is a rectangle
With
AB = PD = 10 m
BD = AP = 12 m
And APC is a right-angled triangle, In ∆APC
`tan theta = "Perpendicular"/"Base" = "CP"/"AP"`
`=> tan 60° = "CP"/12`
`=> sqrt3 = "CP"/12`
⇒ CP = 12√3 m
Also,
CD = CP + PD = (12√3 + 10) m
Hence, height of other building is (10 + 12√3 m).
APPEARS IN
संबंधित प्रश्न
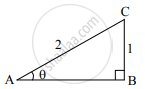
In the following figure, in ΔABC, BC = 1, AC = 2, ∠B = 90°. Find the value of sin θ.
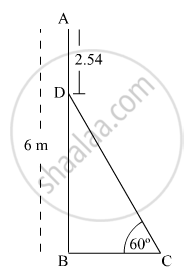
In Fig. 1, AB is a 6 m high pole and CD is a ladder inclined at an angle of 60° to the horizontal and reaches up to a point D of pole. If AD = 2.54 m, find the length of the ladder. (use3√=1.73)
The tops of two towers of height x and y, standing on level ground, subtend angles of 30° and 60° respectively at the centre of the line joining their feet, then find x, y.
A 21 m deep well with diameter 6 m is dug and the earth from digging is evenly spread to form a platform 27 m ✕ 11 m. Find the height of the platform.[Use `pi=22/7`]
A tower stands vertically on the ground. From a point on the ground 20 m away from the foot of the tower, the angle of elevation of the top of the tower is 60°. What is the height of the tower?
A ladder is placed along a wall of a house such that its upper end is touching the top of the wall. The foot of the ladder is 2 m away from the wall and the ladder is making an angle of 60° with the level of the ground. Determine the height of the wall.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff. At a point on the plane 70 metres away from the tower, an observer notices that the angles of elevation of the top and the bottom of the flagstaff are respectively 60° and 45°. Find the height of the flag-staff and that of the tower.
The shadow of a tower, when the angle of elevation of the sun is 45°, is found to be 10 m. longer than when it was 600. Find the height of the tower.
On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 150 m, find the distance between the objects.
From the top of a 15 m high building, the angle of elevation of the top of a tower is found to be 30°. From the bottom of the same building, the angle of elevation of the top of the tower is found to be 60°. Find the height of the tower and the distance between tower and the building.
Find the angle of elevation of the sum (sun's altitude) when the length of the shadow of a vertical pole is equal to its height.
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestones on opposite sides of the aeroplane are observed to be α and β. Show that the height in miles of the aeroplane above the road is given by `(tan alpha tan beta)/(tan alpha + tan beta)`
The angles of depression of the top and bottom of a tower as seen from the top of a 60 `sqrt(3)` m high cliff are 45° and 60° respectively. Find the height of the tower.
Two poles of heights 18 metre and 7 metre are erected on a ground. The length of the wire fastened at their tops in 22 metre. Find the angle made by the wire with the horizontal.
A ladder on the platform of a fire brigade van can be elevated at an angle of 70° to the maximum. The length of the ladder can be extended upto 20 m. If the platform is 2m above the ground, find the maximum height from the ground upto which the ladder can reach. (sin 70° = 0.94)
From a point on the ground, 20 m away from the foot of a vertical tower, the angle elevation of the top of the tower is 60°, What is the height of the tower?
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with horizontal, then the length of the wire is
The angle of elevation of a cloud from a point h metres above a lake is β. The angle of depression of its reflection in the lake is 45°. The height of location of the cloud from the lake is
An aeroplane is flying parallel to the Earth’s surface at a speed of 175 m/sec and at a height of 600 m. The angle of elevation of the aeroplane from a point on the Earth’s surface is 37°. After what period of time does the angle of elevation increase to 53°? (tan 53° = 1.3270, tan 37° = 0.7536)
The top of a hill when observed from the top and bottom of a building of height h is at angles of elevation p and q respectively. What is the height of the hill?
