Advertisements
Advertisements
प्रश्न
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff. At a point on the plane 70 metres away from the tower, an observer notices that the angles of elevation of the top and the bottom of the flagstaff are respectively 60° and 45°. Find the height of the flag-staff and that of the tower.
उत्तर
Let BC be the tower of height x m and AB be the flagstaff of height y, 70 m away from the tower, makes an angle of elevation are 60° and 45° respectively from top and bottom of the flagstaff.
Let AB = y m, BC = x m and CD = 70 m.
So we use trigonometric ratios.
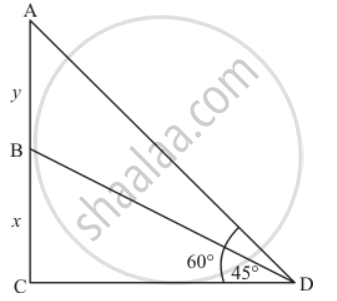
In a triangle BCD
`=> tan D = (BC)/(CD)`
`=> tan 45^@ = x/70`
`=> 1 = 70/x`
`=> x = 70`
Again in a triangle ADC
`=> tan D = (AB + BC)/(CD)`
`=> tan 60^@ = (y + x)/70`
`=> sqrt3 = (y + 70)/70`
`=> 70sqrt3 = 70 + y`
`=> y = 70(sqrt3 - 1)`
=>y = 51.24
Hence the height of flag staff is 51.24 m and height of tower is 70 m
APPEARS IN
संबंधित प्रश्न
Two stations due south of a leaning tower which leans towards the north are at distance a and b from its foot. If α, β be the elevations of the top of the tower from these stations, prove that its inclination θ to the horizontal is given by `\text{cot }\theta =\frac{bcot alpha -a\cot \beta }{b-a}`
The angles of depression of two ships from the top of a lighthouse and on the same side of it are found to be 45° and 30° respectively. If the ships are 200 m apart, find the height of the lighthouse.
An observer, 1.7 m tall, is 203–√203 m away from a tower. The angle of elevation from the of observer to the top of tower is 30°. Find the height of tower ?
Two buildings are in front of each other on either side of a road of width 10 metres. From the top of the first building which is 20 metres high, the angle of elevation to the top of the second is 45°. What is the height of the second building?
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30°. The length of the tower is ____________.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
The angles of depression of two objects from the top of a 100 m hill lying to its east are found to be 45° and 30°. Find the distance between the two objects. (Take `sqrt3 = 1.73`)
If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top remains unchanged.
Two vertical poles of different heights are standing 20m away from each other on the level ground. The angle of elevation of the top of the first pole from the foot of the second pole is 60° and angle of elevation of the top of the second pole from the foot of the first pole is 30°. Find the difference between the heights of two poles. (Take `sqrt(3)` = 1.73)
Read the following passage:
A boy is standing on the top of light house. He observed that boat P and boat Q are approaching the light house from opposite directions. He finds that angle of depression of boat P is 45° and angle of depression of boat Q is 30°. He also knows that height of the light house is 100 m.
|
Based on the above information, answer the following questions.
- What is the measure of ∠APD?
- If ∠YAQ = 30°, then ∠AQD is also 30°, Why?
- Find length of PD
OR
Find length of DQ


