Advertisements
Advertisements
Question
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 5 m. From a point on the ground the angles of elevation of the top and bottom of the flagstaff are 60° and 30° respectively. Find the height of the tower and the distance of the point from the tower. (take\[\sqrt{3}\]= 1.732)
Solution
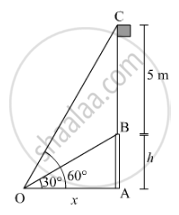
Let AB be the vertical tower and BC be the flagstaff.
Also, let O be the point on the ground from where the angles of elevation of the top and bottom of the flagstaff are 60° and 30°, respectively.
It is given that BC = 5 m.
Let the height of the vertical tower AB be h m and the distance of the point O from the tower be x m.
In ∆OAB,
\[\tan30^o = \frac{AB}{OA}\]
\[ \Rightarrow \frac{1}{\sqrt{3}} = \frac{h}{x}\]
\[ \Rightarrow x = \sqrt{3}h . . . . . \left( 1 \right)\]
In ∆OAC,
\[\tan60^o = \frac{AC}{OA}\]
\[ \Rightarrow \sqrt{3} = \frac{h + 5}{x}\]
\[ \Rightarrow x = \frac{h + 5}{\sqrt{3}} . . . . . \left( 2 \right)\]
From (1) and (2), we get
\[\sqrt{3}h = \frac{h + 5}{\sqrt{3}}\]
\[ \Rightarrow 3h = h + 5\]
\[ \Rightarrow 2h = 5\]
\[ \Rightarrow h = \frac{5}{2} = 2 . 5\]
Thus, the height of the tower is 2.5 m.
Substituting h = 2.5 in (1), we get
APPEARS IN
RELATED QUESTIONS
At a point A, 20 metres above the level of water in a lake, the angle of elevation of a cloud is 30˚. The angle of depression of the reflection of the cloud in the lake, at A is 60˚.
Find the distance of the cloud from A.
A man standing on the deck of a ship, which is 10 m above water level, observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of a hill as 30°. Find the distance of the hill from the ship and the height of the hill
The angle of elevation of a stationary cloud from a point 2500 m above a lake is 15° and the angle of depression of its reflection in the lake is 45°. What is the height of the cloud above the lake level? (Use tan 15° = 0.268)
A storm broke a tree and the tree top rested on ground 20 m away from the
base of the tree, making an angle of 60o with the ground. Find the height
of the tree.
The angle of elevation of a cloud from a point h metre above a lake is θ. The angle of depression of its reflection in the lake is 45°. The height of the cloud is
If sin θ = cos θ , then 2 tan2θ + sin2θ – 1 is equal to
The angles of elevation of the top of the rock from the top and foot of 100 m high tower are respectively 30° and 45°. The height of the rock is ____________.
If two towers of heights h1 and h2 subtend angles of 60° and 30° respectively at the mid-point of the line joining their feet, then h1: h2 = ____________.
A TV tower stands vertically on a bank of a canal, with a height of `10 sqrt3` m. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the distance between the opposite bank of the canal and the point with a 30° angle of elevation.
The angle of elevation of the top of a 15 m high tower at a point `15sqrt(3)` m away from the base of the tower is ______.
