Advertisements
Advertisements
Question
If sin θ = cos θ , then 2 tan2θ + sin2θ – 1 is equal to
Options
`(-3)/2`
`3/2`
`2/3`
`(-2)/3`
Solution
`3/2`
Explanation;
Hint: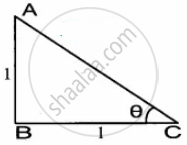
sin θ = cos θ
`sin theta/cos theta` = 1
⇒ tan θ = 1
AC = `sqrt("AB"^2 + "BC"^2)`
= `sqrt(1^2 + 1^2)`
= `sqrt(2)`
sin θ = `1/sqrt(2)`
2 tan2θ + sin2θ − 1 = `2(1)^2 + (1/sqrt(2))^2 - 1`
= `2 + 1/2 - 1`
= `(4 + 1 - 2)/2`
= `(5 - 2)/2`
= `3/2`
APPEARS IN
RELATED QUESTIONS
The heights of two poles are 80 m and 62.5 m. If the line joining their tops makes an angle of 45º with the horizontal, then find the distance between the pole
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff of height 5 meters. At a point on the plane, the angles of elevation of the bottom and the top of the flag-staff are respectively 300 and 600. Find the height of the tower.
A balloon is connected to a meteorological ground station by a cable of length 215 m inclined at 600 to the horizontal. Determine the height of the balloon from the ground. Assume that there is no slack in the cable.
PQ is a post of given height a, and AB is a tower at some distance. If α and β are the angles of elevation of B, the top of the tower, at P and Q respectively. Find the height of the tower and its distance from the post.
The angles of depression of two ships from the top of a lighthouse and on the same side of it are found to be 45° and 30° respectively. If the ships are 200 m apart, find the height of the lighthouse.
The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45 . If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60 , then find the height of the flagstaff [Use `sqrt(3)` 1.732]
The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of depression from the top of the tower to the foot of the hill is 30°. If the tower is 50 m high, find the height of the hill ?
A boy standing at a distance of 48 meters from a building observes the top of the building and makes an angle of elevation of 30°. Find the height of the building.
Two persons are standing ‘x’ metres apart from each other and the height of the first person is double that of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the shorter person (in metres) is
A statue, 2 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point, the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
