Advertisements
Advertisements
प्रश्न
The tops of two towers of height x and y, standing on level ground, subtend angles of 30° and 60° respectively at the centre of the line joining their feet, then find x, y.
उत्तर
Let AB and CD be the two towers of heights x and y, respectively.
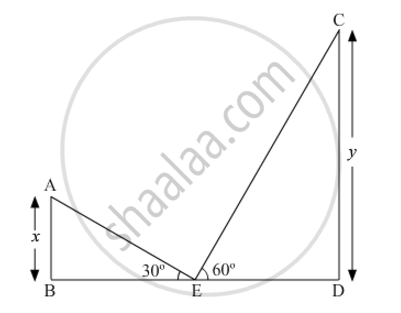
Suppose E is the centre of the line joining the feet of the two towers i.e. BD.
Now, in ∆ABE,
`(AB)/(BE)=tan30^@`
`=>x/(BE)=1/sqrt3`
`=>BE=sqrt3x" ....(1)"`
Also
In ∆CDE,
`(CD)/(DE)=tan60^@`
`=>y/(DE)=sqrt3`
`=>DE=y/sqrt3"....(2)"`
Now, BE = DE .....(3) (E is mid-point of BD.)
So, from (1), (2) and (3), we get
`sqrt3x= y/sqrt3`
`=>x/y=1/3`
Hence, the ratio of x and y is 1 : 3.
APPEARS IN
संबंधित प्रश्न
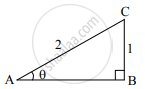
In the following figure, in ΔABC, BC = 1, AC = 2, ∠B = 90°. Find the value of sin θ.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 45°. If the tower is 30 m high, find the height of the building.
A tower is 100√3 metres high. Find the angle of elevation of its top from a point 100 metres away from its foot.
A boy is standing on the ground and flying a kite with 100 m of string at an elevation of 30°. Another boy is sanding on the roof of a 10 m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
An aeroplane at an altitude of 1800 m finds that two boats are sailing towards it in the same direction. The angles of depression of the boats as observed from the aeroplane are 60° and 30° respectively. Find the distance between the two boats. `(sqrt(3) = 1.732)`
The angles of depression of the top and the bottom of a 10 m tall building from the top of a multi-storeyed building are 30° and 45°, respectively. Find the height of the multi-storeyed building.
If a man standing on a platform 3 meters above the surface of a lake observes a cloud and its reflection in the lake, then calculate the angle of elevation of the cloud.
A window of a house is h meters above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be A and B respectively. Then the height of the other house is ____________.
An aeroplane at an altitude of 200 metres observes the angles of depression of opposite points on the two banks of a river to be 45° and 60°. Find the width of the river. (Use = `sqrt(3)` = 1.732)
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 3 m from the banks, find the width of the river. (Use `sqrt(3)` = 1.73)
