Advertisements
Advertisements
Question
The vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height 6m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is
30 and that of the top of the flagstaff 60 . Find the height of the tower
[Use `sqrt(3)` 1.732 ]
Solution
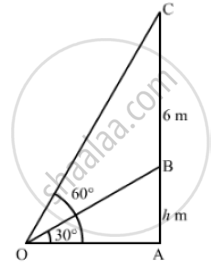
Let AB be the tower and BC be the flagstaff,
We have,
BC = 6m, ∠AOB = 30° and ∠AOC - 60°
Let AB = h
In ΔAOB
`tan 30° = (AB)/(OA)`
`⇒ 1/ sqrt(3) = h/( OA)`
` ⇒ OA = h sqrt(3)` ..............(i)
Now in Δ AOC,
` tan 60° = (AC)/(OA)`
`⇒ sqrt(3) = (AB +BC)/ (h sqrt(3))` [ Using (i)]
⇒ 3h = h + 6
⇒ 3h - h = 6
⇒ 2h = 6
`⇒ h= 6/2`
⇒ h = 3m
So, the height of the tower is 3 m.
APPEARS IN
RELATED QUESTIONS
Two men on either side of the cliff 80 m high observe the angles of an elevation of the top of the cliff to be 30° and 60° respectively. Find the distance between the two men.
Find the angle of elevation of the sum (sun's altitude) when the length of the shadow of a vertical pole is equal to its height.
The angle of elevation of a stationary cloud from a point 2500 m above a lake is 15° and the angle of depression of its reflection in the lake is 45°. What is the height of the cloud above the lake level? (Use tan 15° = 0.268)
Two poles of heights 18 metre and 7 metre are erected on a ground. The length of the wire fastened at their tops in 22 metre. Find the angle made by the wire with the horizontal.
It is found that on walking x meters towards a chimney in a horizontal line through its base, the elevation of its top changes from 30° to 60°. The height of the chimney is
The angle of elevation of the top of a tower at a point on the ground 50 m away from the foot of the tower is 45º. Then the height of the tower (in metres) is
The top of a 15 m high tower makes an angle of elevation of 60° with the bottom of an electronic pole and angle of elevation of 30° with the top of the pole. What is the height of the electric pole?
In given Fig., the angle of depression from the observing position D and E of the object at A are ____________.
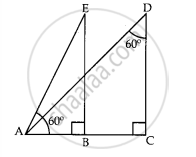
A window of a house is h meters above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be A and B respectively. Then the height of the other house is ____________.
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun is also increasing.
