Advertisements
Advertisements
Question
Two poles of heights 18 metre and 7 metre are erected on a ground. The length of the wire fastened at their tops in 22 metre. Find the angle made by the wire with the horizontal.
Solution
Let AB and CD be the two poles standing on the ground.
Suppose the angle made by the wire with the horizontal be θ.

Here, AB = 18 m and CD = 7 m.
Length of the wire fastened at their tops = AC = 22 m
AE = AB − EB = 18 − 7 = 11 m (EB = CD)
In right ∆AEC,
\[\sin\theta = \frac{AE}{AC}\]
\[ \Rightarrow \sin\theta = \frac{11}{22} = \frac{1}{2}\]
\[ \Rightarrow \sin\theta = \frac{1}{2} = \sin30^\circ\]
\[ \Rightarrow \theta = 30^\circ\]
Thus, the angle made by the wire with the horizontal is 30º.
APPEARS IN
RELATED QUESTIONS
The angle of elevation of the top of a tower from a point A due south of the tower is α and from B due east of the tower is β. If AB = d, show that the height of the tower is
`\frac{d}{\sqrt{\cot ^{2}\alpha +\cot^{2}\beta `
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.

The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of elevation of the top of the tower from the foot of the hill is 30°. If height of the tower is 50 m, find the height of the hill.
The length of a string between a kite and a point on the ground is 90 meters. If the string makes an angle O with the ground level such that tan O = 15/8, how high is the kite? Assume that there is no slack in the string.
The angle of elevation on the top of a building from the foot of a tower is 30° . The angle of elevation of the top of the tower when seen from the top of the second water is 60° .If the tower is 60m high, find the height of the building.
The horizontal distance between two towers is 60 meters. The angle of depression of the top of the first tower when seen from the top of the second tower is 30° . If the height of the second tower is 90 meters. Find the height of the first tower.
The shadow of a tower at a time is three times as long as its shadow when the angle of elevation of the sun is 60°. Find the angle of elevation of the sun at the time of the longer shadow ?
A military tent of height 8.25 m is in the form of a right circular cylinder of base diameter 30 m and height 5.5 m surmounted by a right circular cone of same base radius. Find the length of the canvas used in making the tent, if the breadth of the canvas is 1.5 m.
While landing at an airport, a pilot made an angle of depression of 20°. Average speed of the plane was 200 km/hr. The plane reached the ground after 54 seconds. Find the height at which the plane was when it started landing. (sin 20° = 0.342)
From the top of the tower h metre high , the angles of depression of two objects , which are in the line with the foot of the tower are ∝ and ß (ß> ∝ ) cts .
The angle of elevation of the top of a tower at a point on the ground is 30º. What will be the angle of elevation, if the height of the tower is tripled?
If the angle of elevation of a cloud from a point 200 m above a lake is 30° and the angle of depression of its reflection in the lake is 60°, then the height of the cloud above the lake is
Two buildings are in front of each other on either side of a road of width 10 metres. From the top of the first building which is 20 metres high, the angle of elevation to the top of the second is 45°. What is the height of the second building?
The angle of depression of the top and bottom of 20 m tall building from the top of a multistoried building are 30° and 60° respectively. The height of the multistoried building and the distance between two buildings (in metres) is
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is C to the North of B?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
Two ships are sailing in the sea on either side of the lighthouse. The angles of depression of two ships as observed from the top of the lighthouse are 60° and 45° respectively. If the distance between the ships is `200[(sqrt(3) + 1)/sqrt(3)]` metres, find the height of the lighthouse.
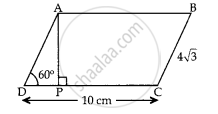
In given figure, ABCD is a || gm. The length of AP is ____________.
An observer 1.5 metres tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.
The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Find the height of the tower.
From the top of an 8 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower. (Take `sqrt(3)` = 1.732).
