Advertisements
Advertisements
Question
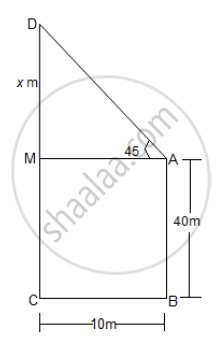
Two building are in front of each other on either side of a road of width 10 metres. From the top of the first building which is 40 metres high, the angle of elevation to the top of the second is 45°. What is the height of the second building?
Solution
Let AB and CD represent two buildings. AB = 40 m, BC is the width of the road.
BC = 10 m
m∠MAD = 45° ---- (angle of elevation)
ABCM is a rectangle.
AM = BC = 10 m ---(1)
AB = MC = 40 m ---(2)
Let MD = x,
Then in right angled ΔAMC,
tan ∠MAD = tan45° = MD/MA
∴ 1 = x/10
∴ x = 10
Now,
CD = CM + MD = 34 + 10 = 50 m.
Thus the height of the second building is 50 m.
APPEARS IN
RELATED QUESTIONS
At a point A, 20 metres above the level of water in a lake, the angle of elevation of a cloud is 30˚. The angle of depression of the reflection of the cloud in the lake, at A is 60˚.
Find the distance of the cloud from A.
A passenger, while boarding the plane, slipped form the stairs and got hurt. The pilot took the passenger in the emergency clinic at the airport for treatment. Due to this, the plane got delayed by half an hour. To reach the destination 1500 km away in time, so that the passengers could catch the connecting flight, the speed of the plane was increased by 250 km/hour than the usual speed. Find the usual speed of the plane
What value is depicted in this question?
A ladder makes an angle of 60° with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder (in metres) is:
(A) `4/sqrt3`
(B) `4sqrt3`
(C) `2sqrt2`
(D)4
Two poles of equal heights are standing opposite each other an either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30º, respectively. Find the height of poles and the distance of the point from the poles.
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
A vertically straight tree, 15 m high, is broken by the wind in such a way that its top just touches the ground and makes an angle of 60° with the ground. At what height from the ground did the tree break?
Two men are on opposite side of tower. They measure the angles of elevation of the top of the tower as 30 and 45 respectively. If the height of the tower is 50 meters, find the distance between the two men.
The radius (in cm) of the largest right circular cone that can be cut out from a cube of edge 4.2 cm is
From a light house the angles of depression of two ships on opposite sides of the light house are observed to be 30° and 45°. If the height of the light house is h metres, the distance between the ships is
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with horizontal, then the length of the wire is
The horizontal distance between two buildings is 70 m. The angle of depression of the top of the first building when seen from the top of the second building is 45°. If the height of the second building is 120 m, find the height of the first building
In given figure, the length of AP is ____________.

In figure given ABCD is a rectangle, the value of CE is ____________.

The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
An observer `sqrt3` m tall is 3 m away from the pole `2 sqrt3` high. What is the angle of elevation of the top?
A vertical pole of 30 m is fixed on a tower. From a point on the level ground, the angle of elevation of the top and bottom of the pole is 60° and 45°. Find the height of the tower.
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun ____________.
The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Find the height of the tower.
A boy 1.7 m tall is standing on a horizontal ground, 50 m away from a building. The angle of elevation of the top of the building from his eye is 60°. Calculate the height of the building. (Take `sqrt(3)` = 1.73)
