Advertisements
Advertisements
प्रश्न
Lakshaman Jhula is located 5 kilometers north-east of the city of Rishikesh in the Indian state of Uttarakhand. The bridge connects the villages of Tapovan to Jonk. Tapovan is in Tehri Garhwal district, on the west bank of the river, while Jonk is in Pauri Garhwal district, on the east bank. Lakshman Jhula is a pedestrian bridge also used by motorbikes. It is a landmark of Rishikesh. A group of Class X students visited Rishikesh in Uttarakhand on a trip. They observed from a point (P) on a river bridge that the angles of depression of opposite banks of the river are 60° and 30° respectively. The height of the bridge is about 18 meters from the river. |
Based on the above information answer the following questions.
- Find the distance PA.
- Find the distance PB
- Find the width AB of the river.
[OR]
Find the height BQ if the angle of the elevation from P to Q be 30°.
उत्तर
I. sin 60° = `(PC)/(PA)`
⇒ `sqrt(3)/2 = 18/(PA)`
⇒ PA = `12sqrt(3)` m
II. sin 30° = `(PC)/(PB)`
⇒ `1/2 = 18/(PB)`
⇒ PB = 36 m
III. tan 60° = `(PC)/(AC)`
⇒ `sqrt(3) = 18/(AC)`
⇒ AC = `6sqrt(3)` m
tan 30° = `(PC)/(CB)`
⇒ `1/sqrt(3) = 18/(CB)`
⇒ CB = `18sqrt(3)` m
Width AB = AC + CB
= `6sqrt(3) + 18sqrt(3)`
= `24sqrt(3)` m
[OR]
RB = PC = 18 m and PR = CB = `18sqrt(3)` m
tan 30° = `(QR)/(PR)`
⇒ `1/sqrt(3) = (QR)/(18sqrt(3))`
⇒ QR = 18 m
QB = QR + RB
= 18 + 18
= 36 m
Hence height BQ is 36 m.
APPEARS IN
संबंधित प्रश्न
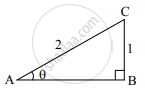
In the following figure, in ΔABC, BC = 1, AC = 2, ∠B = 90°. Find the value of sin θ.
A balloon is connected to a meteorological station by a cable of length 200 m, inclined at 60º to the horizontal. Find the height of the balloon from the ground. Assume that there is no slack in the cable
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.

Two points A and B are on the same side of a tower and in the same straight line with its base. The angles of depression of these points from the top of the tower are 60° and 45° respectively. If the height of the tower is 15 m, then find the distance between the points.
If the angle of elevation of a cloud from a point h meters above a lake is a and the angle of depression of its reflection in the lake be b, prove that the distance of the cloud from the point of observation is `(2h sec alpha)/(tan beta - tan alpha)`
A straight highway leads to the foot of a tower of height 50 m. From the top of the tower, the angles of depression of two cars standing on the highway are 30° and 60° respectively. What is the distance the two cars and how far is each car from the tower?
The angle of depression form the top of a tower of a point A on the ground is 30° . On moving a distance of 20 meters from the point A towards the foot of the tower to a point B, the angle of elevation of the top of the tower to from the point B is 60° . Find the height of the tower and its distance from the point A.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 5 m. From a point on the ground the angles of elevation of the top and bottom of the flagstaff are 60° and 30° respectively. Find the height of the tower and the distance of the point from the tower. (take\[\sqrt{3}\]= 1.732)
A man in a boat rowing away from a lighthouse 100 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 30°.
Find the speed of the boat in metres per minute. [Use `sqrt(3` = 1.732]Use 3=1.732">
A straight highway leads to the foot of a tower. A man standing on the top of the 75 m high tower observes two cars at angles of depression of 30° and 60°, which are approaching the foot of the tower. If one car is exactly behind the other on the same side of the tower, find the distance between the two cars. (use `sqrt(3)` = 1.73)
