Advertisements
Advertisements
प्रश्न
Three villagers A, B and C can see each other using telescope across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30°. Calculate the vertical height between B and C. (tan 20° = 0.3640, `sqrt3` = 1.732)

उत्तर
Let AD is the vertical height between A and B
In the right ∆ABD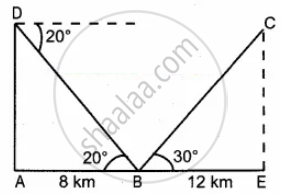
tan 20° = `"AD"/"BD"`
0.3640 = `"AD"/8`
AD = 0.3640 × 8 = 2.912 km
∴ AD = 2.91 km
CE is the vertical height between C and B
In the right ∆BCE, tan 30° = `"CE"/"BE"`
`1/sqrt(3) = "CE"/12`
⇒ `sqrt(3)"CE"` = 12
CE = `12/sqrt(3)`
= `(12 xx sqrt(3))/(sqrt(3) xx sqrt(3))`
= `(12 xx sqrt(3))/3`
= `4sqrt(3)`
= 4 × 1.732
= 6.928
= 6.93 km
The vertical height between B and C = 6.93 km
APPEARS IN
संबंधित प्रश्न
If the elevation of the sun changed from 30º to 60º, then find the difference between the lengths of shadows of a pole 15 m high, made at these two positions
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 5 m. From a point on the ground the angles of elevation of the top and bottom of the flagstaff are 60° and 30° respectively. Find the height of the tower and the distance of the point from the tower. (take\[\sqrt{3}\]= 1.732)
Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angels of elevation of the top of the poles are 60° and 30° respectively.
Find the height of the poles and the distances of the point from the poles.
If the angle of elevation of a cloud from a point 200 m above a lake is 30° and the angle of depression of its reflection in the lake is 60°, then the height of the cloud above the lake is
Find the angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of a tower of height `10sqrt(3)` m
A flag pole ‘h’ metres is on the top of the hemispherical dome of radius ‘r’ metres. A man is standing 7 m away from the dome. Seeing the top of the pole at an angle 45° and moving 5 m away from the dome and seeing the bottom of the pole at an angle 30°. Find the height of the pole `(sqrt(3) = 1.732)`

From the top of a rock `50sqrt(3)` m high, the angle of depression of a car on the ground is observed to be 30°. Find the distance of the car from the rock
In given figure, the length of AP is ____________.

If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top remains unchanged.
