Advertisements
Advertisements
प्रश्न
The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Find the height of the tower.
उत्तर
Let SQ = h be the tower.
∠SPQ = 30° and ∠SRQ = 60°
According to the question,
The length of shadow is 50 m long the angle of elevation of the sun is 30° than when it was 60°.
So, PR = 50 m and RQ = x m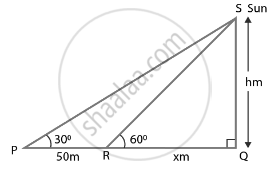
So in ∆SRQ, we have
tan 60° = `"h"/x` ...`[∵ tan θ = "perpendicular"/"base" ⇒ tan 60^circ = "SQ"/"RQ"]`
⇒ `sqrt(3) = "h"/x` ...`[∵ tan 60^circ = sqrt(3)]`
⇒ `x = "h"/sqrt(3)`
In ΔSPQ,
tan 30° = `"h"/(50 + x)` ...`[∵ tan 30^circ = "SQ"/"PQ" = "SQ"/("PR" + "PQ")]`
⇒ `1/sqrt(3) = "h"/(50 + x)` ...`[∵ tan 30^circ = 1/sqrt(3)]`
⇒ `50 + x = sqrt(3)"h"`
Substituting the value of x in the above equation, we get
⇒ `50 + "h"/sqrt(3) = sqrt(3)"h"`
⇒ `(50sqrt(3) + "h")/sqrt(3) = sqrt(3)"h"`
⇒ `50sqrt(3) + "h" = 3"h"`
⇒ `50sqrt(3) = 3"h" - "h"`
⇒ `3"h" - "h" = 50sqrt(3)`
⇒ 2h = `50sqrt(3)`
⇒ h = `(50sqrt(3))/2`
⇒ h = `25sqrt(3)`
Hence, the required height is `25sqrt(3) "m"`.
APPEARS IN
संबंधित प्रश्न
The angle of elevation of a cliff from a fixed point is θ. After going up a distance of k metres towards the top of cliff at an angle of φ, it is found that the angle of elevation is α. Show that the height of the cliff is metres
A vertically straight tree, 15 m high, is broken by the wind in such a way that its top just touches the ground and makes an angle of 60° with the ground. At what height from the ground did the tree break?
A ladder rests against a wall at an angle α to the horizontal. Its foot is pulled away from the wall through a distance a so that it slides a distance b down the wall making an angle β with the horizontal. Show that `a/b = (cos alpha - cos beta)/(sin beta - sin alpha)`
The angle of elevation of an aeroplane from a point on the ground is 45° after flying for 15seconds, the elevation changes to 30° . If the aeroplane is flying at a height of 2500 meters, find the speed of the areoplane.
A boy standing at a distance of 48 meters from a building observes the top of the building and makes an angle of elevation of 30°. Find the height of the building.
From a point on the ground, 20 m away from the foot of a vertical tower, the angle elevation of the top of the tower is 60°, What is the height of the tower?
The horizontal distance between two buildings is 70 m. The angle of depression of the top of the first building when seen from the top of the second building is 45°. If the height of the second building is 120 m, find the height of the first building
The upper part of a tree is broken by the wind and makes an angle of 30° with the ground. The distance from the foot of the tree to the point where the top touches the ground is 5 m. The height of the tree is ____________.
The angle of elevation of the top of a tower from two points distant s and t from its foot are complementary. Prove that the height of the tower is `sqrt(st)`
A boy 1.7 m tall is standing on a horizontal ground, 50 m away from a building. The angle of elevation of the top of the building from his eye is 60°. Calculate the height of the building. (Take `sqrt(3)` = 1.73)
