Advertisements
Advertisements
प्रश्न
Two poles are 'a' metres apart and the height of one is double of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the smaller is
विकल्प
\[\sqrt{2}a \text{ metres }\]
\[\frac{a}{2\sqrt{2}}\text{ metres }\]
\[\frac{a}{\sqrt{2}} \text{ metres }\]
2a metres
उत्तर
Let AB and CD be the two posts such that AB < CD.
Then, let AB = h so that CD = 2h
Now, the given information can be represented as,
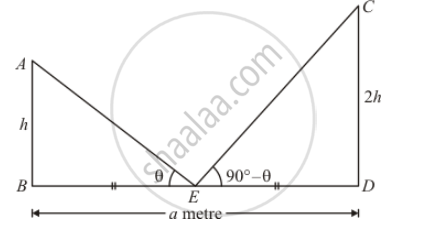
Here, E is the midpoint of BD.
We have to find height of the shorter post.
So we use trigonometric ratios.
In triangle ECD,
`⇒ tan ∠CED=(CD)/(ED)`
`⇒ tan (90°-θ)=(2h)/(a/2)`
`⇒ cot θ=(4h)/a`
Again in triangle ABE,
`⇒ tan ∠AEB=AB/BE`
`⇒ tan θ=h/((a/2))`
` ⇒ 1/cotθ=(2h)/a`
`⇒ a/(4h)=(2h)/a`
`⇒ a^2=8h^2`
`⇒ h=a/(2sqrt2)`
APPEARS IN
संबंधित प्रश्न
A kit is flying at a height of 75 metres from the ground level, attached to a string inclined at 60 to the horizontal. Find the length of the string to the nearest metre.
A TV tower stands vertically on a bank of a river/canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From a point 20 m away this point on the same bank, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the river/canal.
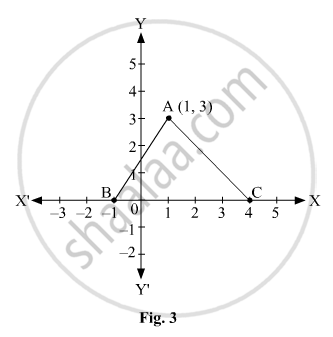
In Fig. 3, the area of triangle ABC (in sq. units) is:
A kite is flying at a height of 30 m from the ground. The length of string from the kite to the ground is 60 m. Assuming that there is no slack in the string, the angle of elevation of the kite at the ground is
A boy standing at a distance of 48 meters from a building observes the top of the building and makes an angle of elevation of 30°. Find the height of the building.
From the top of a light house, the angles of depression of two ships on the opposite sides of it are observed to be α and β. If the height of the light house be h metres and the line joining the ships passes through the foot of the light house, show that the distance between the ship is
`(h (tan ∝+tan ß))/ (tan ∝+tan ∝)`
On a morning walk, three persons step out together and their steps measure 30 cm, 36 cm, and 40 cm respectively. What is the minimum distance each should walk so that each can cover the same distance in complete steps?
If the ratio of the height of a tower and the length of its shadow is `sqrt(3): 1`, then the angle of elevation of the sun has measure
In given figure, AD = 4 cm, BD = 3 cm and CB = 12 cm. The value of tan `theta` is ____________.

The angles of depression of the top and the bottom of a 10 m tall building from the top of a multi-storeyed building are 30° and 45°, respectively. Find the height of the multi-storeyed building.
