Advertisements
Advertisements
Question
If the height of a vertical pole is 3–√3 times the length of its shadow on the ground, then the angle of elevation of the Sun at that time is
(A) 30°
(B) 60°
(C) 45°
(D) 75°
Solution
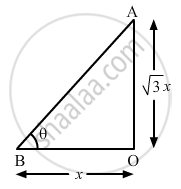
Let AO be the pole and OB be its shadow.
Let the length of the shadow be x.
Let θ be the angle of elevation of the Sun at that time.
Given:
Height of pole (h) =\[\sqrt{3} \times\] Length of its shadow
We have:
\[\tan \theta = \frac{AO}{OB}\]
\[ = \frac{h}{x}\]
\[ = \frac{\sqrt{3}x}{x}\]
\[ = \sqrt{3}\]
\[ \Rightarrow \tan \theta = \tan 60^o\]
\[ \Rightarrow \theta = {60}^\circ\]
Thus, the angle of elevation of the Sun is 60°.
Hence, the correct option is B.
APPEARS IN
RELATED QUESTIONS
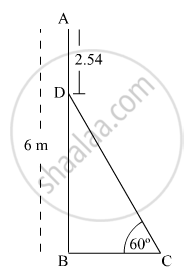
In Fig. 1, AB is a 6 m high pole and CD is a ladder inclined at an angle of 60° to the horizontal and reaches up to a point D of pole. If AD = 2.54 m, find the length of the ladder. (use3√=1.73)
If a vertical pole 6m high has a shadow of length 2 √3 metres, find the angle of elevation of the sun.
The angles of depression of two ships from the top of a lighthouse and on the same side of it are found to be 45° and 30° respectively. If the ships are 200 m apart, find the height of the lighthouse.
From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. The height of the tower is
The tops of two poles of height 16 m and 10 m are connected by a wire of length lmetres. If the wire makes an angle of 30° with the horizontal, then l =
The angle of elevation of the top of a tower at a point on the ground 50 m away from the foot of the tower is 45º. Then the height of the tower (in metres) is
In given figure, the length of AP is ____________.

An observer 1.5 metres tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.
The top of a hill when observed from the top and bottom of a building of height h is at angles of elevation p and q respectively. What is the height of the hill?
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 30°. Determine the height of the tower.
