Question

The perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0) is

(A)\[7 + \sqrt{5}\]
(B) 5
(C) 10
(D) 12

Answer 1

Let us plot these coordinates, i.e. O(0, 0), A(0, 4) and B(3, 0), on the Cartesian plane.

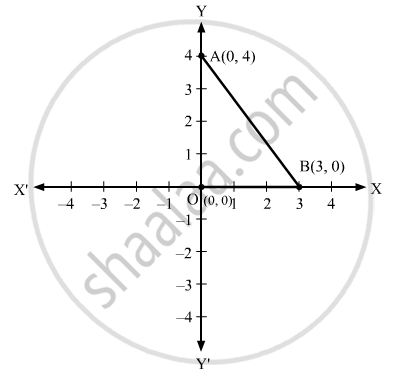
We can observe that triangle AOB is a right-angled triangle with OB = 3 units and OA = 4 units.

Now, AB² = OA² + OB²                  (By Pythagoras theorem)

⇒ AB² = (4² + 3²) sq. units
           = (16 + 9) sq. units
           = 25 sq. units
⇒ AB = 5 units
Perimeter of ∆AOB = OA + AB + BO
                                 = (3 + 5 + 4) units
                                 = 12 units

Hence, the correct option is D.