Advertisements
Advertisements
Question
A rectangular sheet of paper 40 cm × 22 cm, is rolled to form a hollow cylinder of height 40 cm. The radius of the cylinder (in cm) is ______.
Options
3.5
7
\[\frac{80}{7}\]
5
Solution
A rectangular sheet of paper 40 cm × 22 cm, is rolled to form a hollow cylinder of height 40 cm. The radius of the cylinder (in cm) is 3.5.
Explanation:
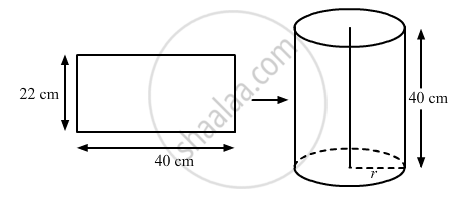
We have,
Length of the rectangular sheet, l = 40 cm,
Width of the rectangular sheet, b = 22 cm and
Height of the hollow cylinder, h = 40 cm
Let the radius of the cylinder be r
As, l = h
So, the circumference of base of the cylinder = b
⇒ 2πr = 22
`=> 2xx22/7xx"r" = 22`
`= "r"=(22xx7)/(2xx22)`
∴ r = 3.5 cm
APPEARS IN
RELATED QUESTIONS
A girl empties a cylindrical bucket, full of sand, of base radius 18 cm and height 32 cm, on the floor to form a conical heap of sand. If the height of this conical heap is 24 cm, then find its slant height correct upto one place of decimal?
A circus tent is in the shape of cylinder surmounted by a conical top of same diameter. If their common diameter is 56 m, the height of the cylindrical part is 6 m and the total height of the tent above the ground is 27 m, find the area of the canvas used in making the tent.
The radii of the ends of a bucket 30 cm high are 21 cm and 7 cm. Find its capacity in litres and the amount of sheet required to make this bucket.
What is the ratio of the volume of a cube to that of a sphere which will fit inside it?
A cylinder, a cone and a hemisphere are of equal base and have the same height. What is the ratio of their volumes?
The curved surface area of a sphere is 5544 cm2. Find its volume.
The interior of a building is in the form of a right circular cylinder of diameter 4.2 m and height 4 m surmounted by a cone of same diameter.
The height of the cone is 2.8 m. Find the outer surface area of the building.
The radii of the top and bottom of a bucket of slant height 45cm are 28cm and 7 cm respectively. The curved surface area of the bucket is ______.
Match the column:
| (1) surface area of cuboid | (A) πr2h |
| (2) surface area of closed right cylinder | (B) 2πr(h + r) |
| (3) Total surface area of right cone | (C) πrl + πr2 |
| (4) Total surface area of hemisphere | (D) 3πr3 |
| (E) 3πr2 | |
| (F) 2[lb + bh + lh] |
Two identical cubes each of volume 64 cm3 are joined together end to end. What is the surface area of the resulting cuboid?
