Question

A rectangular sheet of paper 40 cm × 22 cm, is rolled to form a hollow cylinder of height 40 cm. The radius of the cylinder (in cm) is ______.

विकल्प

•  3.5

• 7

• \[\frac{80}{7}\]

• 5

Answer 1

A rectangular sheet of paper 40 cm × 22 cm, is rolled to form a hollow cylinder of height 40 cm. The radius of the cylinder (in cm) is 3.5.

Explanation:

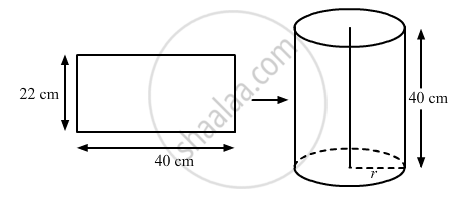
We have,

Length of the rectangular sheet, l = 40 cm,

Width of the rectangular sheet, b = 22 cm and 

Height of the hollow cylinder, h = 40 cm

Let the radius of the cylinder be r 

As, l = h

So, the circumference of base of the cylinder = b

⇒ 2πr = 22

`=> 2xx22/7xx"r" = 22`

`= "r"=(22xx7)/(2xx22)`

∴ r = 3.5 cm