Advertisements
Advertisements
Question
Find the length diagonal of a rectangle whose length is 35 cm and breadth is 12 cm.
Solution
`square`ABCD is a rectangle
`l(AB) = 35 cm`
`l(BC) = 12 cm`
Let AC be the diagonal of rectangle
as ∠A = ∠B = ∠C = ∠D = 90°
∴ In `triangle`ABC, as ∠B = 90°
∴ By using Pythagoras theorem.
`AC^2 = AB^2 + BC^2`
`AC^2 = 35^2 + 12^2`
`AC^2 = 1225 + 144`
`AC^2 =1369`
`AC =37cm`
∴ The diagonal of the rectangle is 37 cm.
RELATED QUESTIONS
A man goes 10 m due east and then 24 m due north. Find the distance from the starting point
ABC is an isosceles triangle with AC = BC. If AB2 = 2AC2, prove that ABC is a right triangle.
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals
In the given figure, ABC is a triangle in which ∠ABC < 90° and AD ⊥ BC. Prove that AC2 = AB2 + BC2 − 2BC.BD.

In an isosceles triangle, length of the congruent sides is 13 cm and its base is 10 cm. Find the distance between the vertex opposite the base and the centroid.
In a trapezium ABCD, seg AB || seg DC seg BD ⊥ seg AD, seg AC ⊥ seg BC, If AD = 15, BC = 15 and AB = 25. Find A(▢ABCD)

Prove that `(sin θ + cosec θ)^2 + (cos θ + sec θ)^2 = 7 + tan^2 θ + cot^2 θ`.
Prove that (1 + cot A - cosec A ) (1 + tan A + sec A) = 2
Prove that in a right angle triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.
In ∆ ABC, AD ⊥ BC.
Prove that AC2 = AB2 +BC2 − 2BC x BD
In the given figure, angle ACB = 90° = angle ACD. If AB = 10 m, BC = 6 cm and AD = 17 cm, find :
(i) AC
(ii) CD

Calculate the area of a right-angled triangle whose hypotenuse is 65cm and one side is 16cm.
In ΔABC, AD is perpendicular to BC. Prove that: AB2 + CD2 = AC2 + BD2
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = AE2 + CD2 + BF2
A point OI in the interior of a rectangle ABCD is joined with each of the vertices A, B, C and D. Prove that OB2 + OD2 = OC2 + OA2
Determine whether the triangle whose lengths of sides are 3 cm, 4 cm, 5 cm is a right-angled triangle.
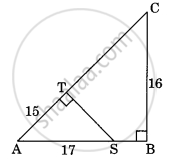
In the given figure, ∠T and ∠B are right angles. If the length of AT, BC and AS (in centimeters) are 15, 16, and 17 respectively, then the length of TC (in centimeters) is ______.
Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
Two squares are congruent, if they have same ______.
