Advertisements
Advertisements
Question
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = AE2 + CD2 + BF2
Solution
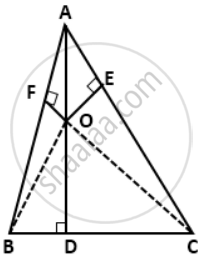
In right triangles ODB and ODC, we have
OB2 = OD2 + BD2
OC2 = OD2 + CD2
∴ OB2 - OC2 = (OD2 + BD2) - (OD2 + CD2)
⇒ OB2 - OC2 = BD2 - CD2 ....(i)
Similarly, we have
OC2 - OA2 = CE2 - AE2 ....(ii)
OA2 - OB2 = AF2 - BF2 ....(iii)
Adding (i), (ii) and (iii), we get
(OB2 - OC2) + (OC2 - OA2) + (OA2 - OB2) = (BD2 - CD2) + (CE2 - AE2) + (AF2 - BF2)
⇒ (BD2 + CE2 + AF2) - (AE2 + CD2 + BF2) = 0
⇒ AF2 + BD2 + CE2 = AE2 + CD2 + BF2.
APPEARS IN
RELATED QUESTIONS
A ladder leaning against a wall makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder
In Fig., ∆ABC is an obtuse triangle, obtuse angled at B. If AD ⊥ CB, prove that AC2 = AB2 + BC2 + 2BC × BD
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 7 cm, 24 cm, 25 cm
ABC is an isosceles triangle right angled at C. Prove that AB2 = 2AC2
ABC is a triangle right angled at C. If AB = 25 cm and AC = 7 cm, find BC.
Prove that the points A(0, −1), B(−2, 3), C(6, 7) and D(8, 3) are the vertices of a rectangle ABCD?
Identify, with reason, if the following is a Pythagorean triplet.
(10, 24, 27)
In the given figure, ∠DFE = 90°, FG ⊥ ED, If GD = 8, FG = 12, find (1) EG (2) FD and (3) EF

In the following figure, OP, OQ, and OR are drawn perpendiculars to the sides BC, CA and AB respectively of triangle ABC.
Prove that: AR2 + BP2 + CQ2 = AQ2 + CP2 + BR2

Choose the correct alternative:
In right-angled triangle PQR, if hypotenuse PR = 12 and PQ = 6, then what is the measure of ∠P?
If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2 ) = (AB2 + PQ2)
In triangle PQR, angle Q = 90°, find: PQ, if PR = 34 cm and QR = 30 cm
The sides of the triangle are given below. Find out which one is the right-angled triangle?
1.5, 1.6, 1.7
Two poles of height 9m and 14m stand on a plane ground. If the distance between their 12m, find the distance between their tops.
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = OA2 + OB2 + OC2 - OD2 - OE2 - OF2
∆ABC is right-angled at C. If AC = 5 cm and BC = 12 cm. find the length of AB.
If ‘l‘ and ‘m’ are the legs and ‘n’ is the hypotenuse of a right angled triangle then, l2 = ________
In a right angled triangle, if length of hypotenuse is 25 cm and height is 7 cm, then what is the length of its base?
If ΔABC ~ ΔPQR, `("ar" triangle "ABC")/("ar" triangle "PQR") = 9/4` and AB = 18 cm, then the length of PQ is ______.
For going to a city B from city A, there is a route via city C such that AC ⊥ CB, AC = 2x km and CB = 2(x + 7) km. It is proposed to construct a 26 km highway which directly connects the two cities A and B. Find how much distance will be saved in reaching city B from city A after the construction of the highway.
