Advertisements
Advertisements
प्रश्न
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = AE2 + CD2 + BF2
उत्तर
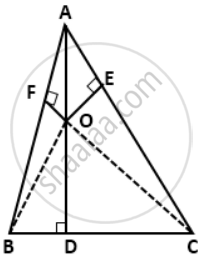
In right triangles ODB and ODC, we have
OB2 = OD2 + BD2
OC2 = OD2 + CD2
∴ OB2 - OC2 = (OD2 + BD2) - (OD2 + CD2)
⇒ OB2 - OC2 = BD2 - CD2 ....(i)
Similarly, we have
OC2 - OA2 = CE2 - AE2 ....(ii)
OA2 - OB2 = AF2 - BF2 ....(iii)
Adding (i), (ii) and (iii), we get
(OB2 - OC2) + (OC2 - OA2) + (OA2 - OB2) = (BD2 - CD2) + (CE2 - AE2) + (AF2 - BF2)
⇒ (BD2 + CE2 + AF2) - (AE2 + CD2 + BF2) = 0
⇒ AF2 + BD2 + CE2 = AE2 + CD2 + BF2.
APPEARS IN
संबंधित प्रश्न
In figure, ∠B of ∆ABC is an acute angle and AD ⊥ BC, prove that AC2 = AB2 + BC2 – 2BC × BD
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2 + BD2 = AB2 + DE2
Prove that the points A(0, −1), B(−2, 3), C(6, 7) and D(8, 3) are the vertices of a rectangle ABCD?
In the figure: ∠PSQ = 90o, PQ = 10 cm, QS = 6 cm and RQ = 9 cm. Calculate the length of PR.
In the given figure, ∠B = 90°, XY || BC, AB = 12 cm, AY = 8cm and AX : XB = 1 : 2 = AY : YC.
Find the lengths of AC and BC.

Prove that (1 + cot A - cosec A ) (1 + tan A + sec A) = 2
The sides of a certain triangle is given below. Find, which of them is right-triangle
6 m, 9 m, and 13 m
In the given figure, angle BAC = 90°, AC = 400 m, and AB = 300 m. Find the length of BC.

The sides of the triangle are given below. Find out which one is the right-angled triangle?
11, 12, 15
Find the length of the perpendicular of a triangle whose base is 5cm and the hypotenuse is 13cm. Also, find its area.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 = AD2 - BC x CE + `(1)/(4)"BC"^2`
A point OI in the interior of a rectangle ABCD is joined with each of the vertices A, B, C and D. Prove that OB2 + OD2 = OC2 + OA2
PQR is an isosceles triangle with PQ = PR = 10 cm and QR = 12 cm. Find the length of the perpendicular from P to QR.
From given figure, In ∆ABC, If AC = 12 cm. then AB =?

Activity: From given figure, In ∆ABC, ∠ABC = 90°, ∠ACB = 30°
∴ ∠BAC = `square`
∴ ∆ABC is 30° – 60° – 90° triangle
∴ In ∆ABC by property of 30° – 60° – 90° triangle.
∴ AB = `1/2` AC and `square` = `sqrt(3)/2` AC
∴ `square` = `1/2 xx 12` and BC = `sqrt(3)/2 xx 12`
∴ `square` = 6 and BC = `6sqrt(3)`
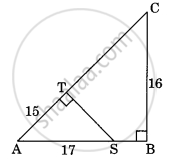
In the given figure, ∠T and ∠B are right angles. If the length of AT, BC and AS (in centimeters) are 15, 16, and 17 respectively, then the length of TC (in centimeters) is ______.
Lengths of sides of a triangle are 3 cm, 4 cm and 5 cm. The triangle is ______.
In a triangle, sum of squares of two sides is equal to the square of the third side.
If two legs of a right triangle are equal to two legs of another right triangle, then the right triangles are congruent.
Jayanti takes shortest route to her home by walking diagonally across a rectangular park. The park measures 60 metres × 80 metres. How much shorter is the route across the park than the route around its edges?
