Advertisements
Advertisements
Question
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that: 9AQ2 = 9AC2 + 4BC2
Solution
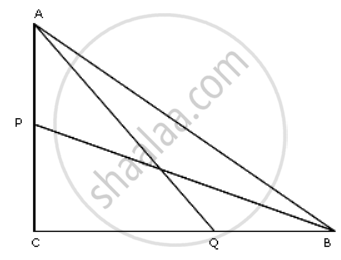
P divides AC in the ratio 2 : 1
So C.P. = `(2)/(3) "AC"` .......(i)
Q divides BC in the ratio 2 : 1
QC = `(2)/(3)"BC"` ......(ii)
In ΔACQ
Using Pythagoras Theorem we have,
AQ2 + AC2 + CQ2
⇒ AQ2 = `"AC"^2 + (4)/(9)"BC"^2` ...(using (ii))
⇒ 9AQ2 = 9AC2 + 4BC2. ......(iii)
APPEARS IN
RELATED QUESTIONS
In a right triangle ABC right-angled at C, P and Q are the points on the sides CA and CB respectively, which divide these sides in the ratio 2 : 1. Prove that
`(i) 9 AQ^2 = 9 AC^2 + 4 BC^2`
`(ii) 9 BP^2 = 9 BC^2 + 4 AC^2`
`(iii) 9 (AQ^2 + BP^2 ) = 13 AB^2`
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 50 cm, 80 cm, 100 cm
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AD2 = BD × CD

ABC is an isosceles triangle right angled at C. Prove that AB2 = 2AC2
Tick the correct answer and justify: In ΔABC, AB = `6sqrt3` cm, AC = 12 cm and BC = 6 cm.
The angle B is:
In the given figure, ∆ABC is an equilateral triangle of side 3 units. Find the coordinates of the other two vertices ?

Walls of two buildings on either side of a street are parallel to each other. A ladder 5.8 m long is placed on the street such that its top just reaches the window of a building at the height of 4 m. On turning the ladder over to the other side of the street, its top touches the window of the other building at a height 4.2 m. Find the width of the street.
In right angle ΔABC, if ∠B = 90°, AB = 6, BC = 8, then find AC.
Triangle XYZ is right-angled at vertex Z. Calculate the length of YZ, if XY = 13 cm and XZ = 12 cm.
In the given figure, angle BAC = 90°, AC = 400 m, and AB = 300 m. Find the length of BC.

Use the information given in the figure to find the length AD.

Calculate the area of a right-angled triangle whose hypotenuse is 65cm and one side is 16cm.
In ΔABC, AD is perpendicular to BC. Prove that: AB2 + CD2 = AC2 + BD2
In a right-angled triangle PQR, right-angled at Q, S and T are points on PQ and QR respectively such as PT = SR = 13 cm, QT = 5 cm and PS = TR. Find the length of PQ and PS.
If in a ΔPQR, PR2 = PQ2 + QR2, then the right angle of ∆PQR is at the vertex ________
Find the unknown side in the following triangles
Rithika buys an LED TV which has a 25 inches screen. If its height is 7 inches, how wide is the screen? Her TV cabinet is 20 inches wide. Will the TV fit into the cabinet? Give reason
In a triangle, sum of squares of two sides is equal to the square of the third side.
Two squares having same perimeter are congruent.
The hypotenuse (in cm) of a right angled triangle is 6 cm more than twice the length of the shortest side. If the length of third side is 6 cm less than thrice the length of shortest side, then find the dimensions of the triangle.
