Advertisements
Advertisements
प्रश्न
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that: 9AQ2 = 9AC2 + 4BC2
उत्तर
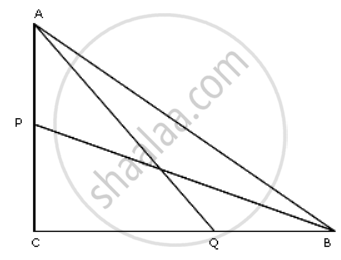
P divides AC in the ratio 2 : 1
So C.P. = `(2)/(3) "AC"` .......(i)
Q divides BC in the ratio 2 : 1
QC = `(2)/(3)"BC"` ......(ii)
In ΔACQ
Using Pythagoras Theorem we have,
AQ2 + AC2 + CQ2
⇒ AQ2 = `"AC"^2 + (4)/(9)"BC"^2` ...(using (ii))
⇒ 9AQ2 = 9AC2 + 4BC2. ......(iii)
APPEARS IN
संबंधित प्रश्न
The diagonal of a rectangular field is 16 metres more than the shorter side. If the longer side is 14 metres more than the shorter side, then find the lengths of the sides of the field.
If ABC is an equilateral triangle of side a, prove that its altitude = ` \frac { \sqrt { 3 } }{ 2 } a`
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.
Prove that, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the square of remaining two sides
Identify, with reason, if the following is a Pythagorean triplet.
(5, 12, 13)

In ΔMNP, ∠MNP = 90˚, seg NQ ⊥ seg MP, MQ = 9, QP = 4, find NQ.
In the figure, given below, AD ⊥ BC.
Prove that: c2 = a2 + b2 - 2ax.
In a rectangle ABCD,
prove that: AC2 + BD2 = AB2 + BC2 + CD2 + DA2.
Find the length of diagonal of the square whose side is 8 cm.
In the given figure, angle BAC = 90°, AC = 400 m, and AB = 300 m. Find the length of BC.

A ladder 25m long reaches a window of a building 20m above the ground. Determine the distance of the foot of the ladder from the building.
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = AE2 + CD2 + BF2
The perpendicular PS on the base QR of a ∆PQR intersects QR at S, such that QS = 3 SR. Prove that 2PQ2 = 2PR2 + QR2
In the figure, find AR
Choose the correct alternative:
If length of sides of a triangle are a, b, c and a2 + b2 = c2, then which type of triangle it is?
In the adjoining figure, a tangent is drawn to a circle of radius 4 cm and centre C, at the point S. Find the length of the tangent ST, if CT = 10 cm.

The longest side of a right angled triangle is called its ______.
If the areas of two circles are the same, they are congruent.
Jayanti takes shortest route to her home by walking diagonally across a rectangular park. The park measures 60 metres × 80 metres. How much shorter is the route across the park than the route around its edges?
