Advertisements
Advertisements
Question
Rithika buys an LED TV which has a 25 inches screen. If its height is 7 inches, how wide is the screen? Her TV cabinet is 20 inches wide. Will the TV fit into the cabinet? Give reason
Solution
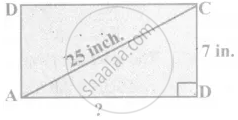
Take the sides of a right angled triangle ∆ABC as
a = 7 inches
b = 25 inches
c = ?
By Pythagoras theorem,
b2 = a2 + c2
252 = 72 + c2
⇒ c2 = 252 – 72
= 625 – 49 = 576
∴ c2 = 242
⇒ c = 24 inches
∴ Width of TV cabinet is 20 inches which is lesser than the width of the screen ie. 24 inches.
∴ The TV will not fit into the cabinet.
APPEARS IN
RELATED QUESTIONS
Prove that the diagonals of a rectangle ABCD, with vertices A(2, -1), B(5, -1), C(5, 6) and D(2, 6), are equal and bisect each other.
Two towers of heights 10 m and 30 m stand on a plane ground. If the distance between their feet is 15 m, find the distance between their tops
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
In triangle ABC, AB = AC and BD is perpendicular to AC.
Prove that: BD2 - CD2 = 2CD × AD
If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2 ) = (AB2 + PQ2)
The foot of a ladder is 6m away from a wall and its top reaches a window 8m above the ground. If the ladder is shifted in such a way that its foot is 8m away from the wall to what height does its tip reach?
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = OA2 + OB2 + OC2 - OD2 - OE2 - OF2
The perpendicular PS on the base QR of a ∆PQR intersects QR at S, such that QS = 3 SR. Prove that 2PQ2 = 2PR2 + QR2
Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.
Height of a pole is 8 m. Find the length of rope tied with its top from a point on the ground at a distance of 6 m from its bottom.
