Advertisements
Advertisements
प्रश्न
Rithika buys an LED TV which has a 25 inches screen. If its height is 7 inches, how wide is the screen? Her TV cabinet is 20 inches wide. Will the TV fit into the cabinet? Give reason
उत्तर
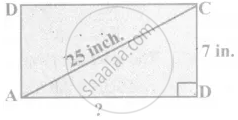
Take the sides of a right angled triangle ∆ABC as
a = 7 inches
b = 25 inches
c = ?
By Pythagoras theorem,
b2 = a2 + c2
252 = 72 + c2
⇒ c2 = 252 – 72
= 625 – 49 = 576
∴ c2 = 242
⇒ c = 24 inches
∴ Width of TV cabinet is 20 inches which is lesser than the width of the screen ie. 24 inches.
∴ The TV will not fit into the cabinet.
APPEARS IN
संबंधित प्रश्न
ABC is an isosceles triangle with AC = BC. If AB2 = 2AC2, prove that ABC is a right triangle.
Digonals of parallelogram WXYZ intersect at point O. If OY =5, find WY.
In the given figure, ∠B = 90°, XY || BC, AB = 12 cm, AY = 8cm and AX : XB = 1 : 2 = AY : YC.
Find the lengths of AC and BC.

In equilateral Δ ABC, AD ⊥ BC and BC = x cm. Find, in terms of x, the length of AD.
In Fig. 3, ∠ACB = 90° and CD ⊥ AB, prove that CD2 = BD x AD.

Show that the triangle ABC is a right-angled triangle; if: AB = 9 cm, BC = 40 cm and AC = 41 cm
In the figure below, find the value of 'x'.

From given figure, In ∆ABC, If AC = 12 cm. then AB =?

Activity: From given figure, In ∆ABC, ∠ABC = 90°, ∠ACB = 30°
∴ ∠BAC = `square`
∴ ∆ABC is 30° – 60° – 90° triangle
∴ In ∆ABC by property of 30° – 60° – 90° triangle.
∴ AB = `1/2` AC and `square` = `sqrt(3)/2` AC
∴ `square` = `1/2 xx 12` and BC = `sqrt(3)/2 xx 12`
∴ `square` = 6 and BC = `6sqrt(3)`
Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
Two squares having same perimeter are congruent.
