Advertisements
Advertisements
Question
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
Solution
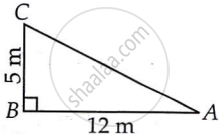
In the given figure, BC represents the unbroken part of the tree. Point C represents the point where the tree broke and CA represents the broken part of the tree. Triangle ABC, thus formed, is right-angled at B.
Applying Pythagoras theorem in ΔABC,
AC2 = BC2 + AB2
AC2 = (5 m)2 + (12 m)2
AC2 = 25 m2 + 144 m2
AC2 = 169 m2
AC = 13 m
Thus, original height of the tree = AC + CB
= 13 m + 5 m
= 18 m
APPEARS IN
RELATED QUESTIONS
In the given figure, ABC is a triangle in which ∠ABC < 90° and AD ⊥ BC. Prove that AC2 = AB2 + BC2 − 2BC.BD.

Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.
In the given figure, ∠DFE = 90°, FG ⊥ ED, If GD = 8, FG = 12, find (1) EG (2) FD and (3) EF

In the given figure, M is the midpoint of QR. ∠PRQ = 90°. Prove that, PQ2 = 4PM2 – 3PR2.

Find the length of the hypotenuse of a right angled triangle if remaining sides are 9 cm and 12 cm.
In triangle ABC, ∠B = 90o and D is the mid-point of BC.
Prove that: AC2 = AD2 + 3CD2.
In a square PQRS of side 5 cm, A, B, C and D are points on sides PQ, QR, RS and SP respectively such as PA = PD = RB = RC = 2 cm. Prove that ABCD is a rectangle. Also, find the area and perimeter of the rectangle.
Choose the correct alternative:
If length of sides of a triangle are a, b, c and a2 + b2 = c2, then which type of triangle it is?
For going to a city B from city A, there is a route via city C such that AC ⊥ CB, AC = 2x km and CB = 2(x + 7) km. It is proposed to construct a 26 km highway which directly connects the two cities A and B. Find how much distance will be saved in reaching city B from city A after the construction of the highway.
A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
