Advertisements
Advertisements
प्रश्न
A tower stands vertically on the ground. From a point on the ground which is 20 m away from the foot of the tower, the angle of elevation of its top is found to be 60°. Find the height of the tower. [Take `sqrt(3)` =1.732 ]
उत्तर
Let AB be the tower standing vertically on the ground and O be the position of the obsrever we now have:
OA = 20m, ∠OAB = 90° and ∠AOB = 60°
Let
AB = hm
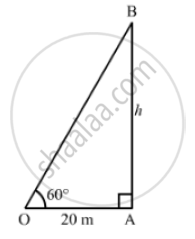
Now, in the right ΔOAB,we have:
`(AB)/(OA)- tan 60° = sqrt(3)`
`⇒ h/20 = sqrt(3)`
`⇒ h = 20 sqrt(3) = (20 xx 1.732 ) = 36.64`
Hence, the height of the pole is 34.64 m.
APPEARS IN
संबंधित प्रश्न
If the angle of elevation of a cloud from a point h metres above a lake is α and the angle of depression of its reflection in the lake is β, prove that the height of the cloud is
`\frac{h(\tan\alpha +\tan \beta )}{\tan \beta -\tan \alpha }`
The angle of elevation of a cliff from a fixed point is θ. After going up a distance of k metres towards the top of cliff at an angle of φ, it is found that the angle of elevation is α. Show that the height of the cliff is metres
A man sitting at a height of 20 m on a tall tree on a small island in the middle of a river observes two poles directly opposite to each other on the two banks of the river and in line with the foot of the tree. If the angles of depression of the feet of the poles from a point at which the man is sitting on the tree on either side of the river are 60° and 30°respectively. Find the width of the river.
The length of the shadow of a tower standing on the level plane is found to 2x meter longer when the sun's altitude is 30° than when it was 45°. Prove that the height of the tower is `x(sqrt3 + 1)` meters.
A tree breaks due to the storm and the broken part bends so that the top of the tree touches the ground making an angle of 30° with the ground. The distance from the foot of the tree to the point where the top touches the ground is 10 metres. Find the height of the tree.
It is found that on walking x meters towards a chimney in a horizontal line through its base, the elevation of its top changes from 30° to 60°. The height of the chimney is
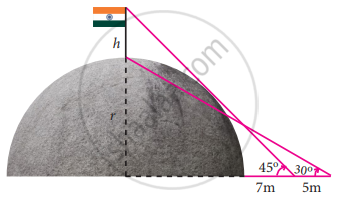
A flag pole ‘h’ metres is on the top of the hemispherical dome of radius ‘r’ metres. A man is standing 7 m away from the dome. Seeing the top of the pole at an angle 45° and moving 5 m away from the dome and seeing the bottom of the pole at an angle 30°. Find the height of the pole `(sqrt(3) = 1.732)`
Read the following passage and answer the questions given below.
|
Kite Festival Kite festival is celebrated in many countries at different times of the year. In India, every year 14th January is celebrated as International Kite Day. On this day many people visit India and participate in the festival by flying various kinds of kites. The picture given below, show three kites flying together.
In the given figure, the angles of elevation of two kites (Points A and B) from the hands of a man (Point C) are found to be 30° and 60° respectively. Taking AD = 50 m and BE = 60 m, find. |
- the lengths of strings used (take them straight) for kites A and B as shown in the figure.
- the distance 'd' between these two kites.
From the base of a pole of height 20 meter, the angle of elevation of the top of a tower is 60°. The pole subtends an angle 30° at the top of tower. Then the height of tower is ______.
The angle of elevation of the top P of a vertical tower PQ of height 10 from a point A on the horizontal ground is 45°. Let R be a point on AQ and from a point B, vertically above R, the angle of elevation of P is 60°. If ∠BAQ = 30°, AB = d and the area of the trapezium PQRB is α, then the ordered pair (d, α) is ______.


