Advertisements
Advertisements
प्रश्न
A military tent of height 8.25 m is in the form of a right circular cylinder of base diameter 30 m and height 5.5 m surmounted by a right circular cone of same base radius. Find the length of the canvas used in making the tent, if the breadth of the canvas is 1.5 m.
उत्तर
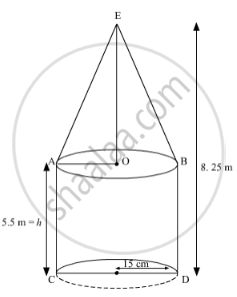
It is given that, radius of cylinder `(r_1)=30/2m=15m`
Height of cylinder (h1) = 5.5 m
And, height of the tent (H) = 8.25 m
So, height of cone (h2) = 8.25 m − 5.50 m = 2.75 m
And, radius of cone (r2) = 15 m
Let the slant height of the cone be l m.
`therefore l^2=(15m)^2+(2.75m)^2`
`rArr l^2=(225+7.5625)m^2`
`rArr l=sqrt232.5625m`
`rArrl=15.25 m`
Curved surface area of the tent = Curved surface area of cylinder + Curved surface area
of cone
`=2pir_1h_1+pir_2l`
`=(2xx22/7xx15xx5.5)cm^2+22/7xx15xx15.25cm^2`
`=(518.57+718.93)cm^2`
`=1237.5m^2`
Now, curved surface area of the tent is equal to the area of rectangular piece of canvas.
It is given that, breadth of canvas = 1.5 m
Let l be the length of canvas.
∴l × 1.5 = 1237.5
`rArrl=1237.5/1.5=825m`
Hence, the length of canvas used in making the tent is 825 m.
APPEARS IN
संबंधित प्रश्न
Two ships are there in the sea on either side of a light house in such a way that the ships and the light house are in the same straight line. The angles of depression of two ships as observed from the top of the light house are 60° and 45°. If the height of the light house is 200 m, find the distance between the two ships. [use √3=1.73]
At the foot of a mountain the elevation of its summit is 45º; after ascending 1000 m towards the mountain up a slope of 30º inclination is found to be 60º. Find the height of the mountain.
PQ is a post of given height a, and AB is a tower at some distance. If α and β are the angles of elevation of B, the top of the tower, at P and Q respectively. Find the height of the tower and its distance from the post.
Two boats approach a lighthouse in mid-sea from opposite directions. The angles of elevation of the top of the lighthouse from two boats are 30° and 45° respectively. If the distance between two boats is 100 m, find the height of the lighthouse.
A ladder of length 6meters makes an angle of 45° with the floor while leaning against one wall of a room. If the fort of the ladder is kept fixed on the floor and it is made to lean against the opposite wall of the room, it makes an angle of 60° with the floor. Find the
distance between two walls of the room.
If the ratio of the height of a tower and the length of its shadow is `sqrt(3): 1`, then the angle of elevation of the sun has measure
In given figure, AD = 4 cm, BD = 3 cm and CB = 12 cm. The value of tan `theta` is ____________.

The upper part of a tree is broken by the wind and makes an angle of 30° with the ground. The distance from the foot of the tree to the point where the top touches the ground is 5 m. The height of the tree is ____________.
If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top ____________.
The angle of elevation of the top P of a vertical tower PQ of height 10 from a point A on the horizontal ground is 45°. Let R be a point on AQ and from a point B, vertically above R, the angle of elevation of P is 60°. If ∠BAQ = 30°, AB = d and the area of the trapezium PQRB is α, then the ordered pair (d, α) is ______.
