Advertisements
Advertisements
प्रश्न
A military tent of height 8.25 m is in the form of a right circular cylinder of base diameter 30 m and height 5.5 m surmounted by a right circular cone of same base radius. Find the length of the canvas used in making the tent, if the breadth of the canvas is 1.5 m.
उत्तर
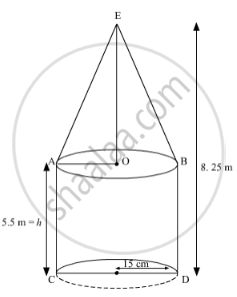
It is given that, radius of cylinder `(r_1)=30/2m=15m`
Height of cylinder (h1) = 5.5 m
And, height of the tent (H) = 8.25 m
So, height of cone (h2) = 8.25 m − 5.50 m = 2.75 m
And, radius of cone (r2) = 15 m
Let the slant height of the cone be l m.
`therefore l^2=(15m)^2+(2.75m)^2`
`rArr l^2=(225+7.5625)m^2`
`rArr l=sqrt232.5625m`
`rArrl=15.25 m`
Curved surface area of the tent = Curved surface area of cylinder + Curved surface area
of cone
`=2pir_1h_1+pir_2l`
`=(2xx22/7xx15xx5.5)cm^2+22/7xx15xx15.25cm^2`
`=(518.57+718.93)cm^2`
`=1237.5m^2`
Now, curved surface area of the tent is equal to the area of rectangular piece of canvas.
It is given that, breadth of canvas = 1.5 m
Let l be the length of canvas.
∴l × 1.5 = 1237.5
`rArrl=1237.5/1.5=825m`
Hence, the length of canvas used in making the tent is 825 m.
APPEARS IN
संबंधित प्रश्न
If a vertical pole 6m high has a shadow of length 2 √3 metres, find the angle of elevation of the sun.
The pilot of a helicopter, at an altitude of 1200m finds that the two ships are sailing towards it in the same direction. The angle of depression of the ships as observed from the helicopter are 60º and 45º respectively. Find the distance between the two ships
The angle of elevation of the top of a vertical tower from a point on the ground is 60° . From another point 10 m vertically above the first, its angle of elevation is 30° .Find the height of the tower.
A storm broke a tree and the treetop rested 20 m from the base of the tree, making an angle of 60° with the horizontal. Find the height of the tree.
The angles of depression of two ships from the top of a light house are 45° and 30° towards east. If the ships are 100 m apart. the height of the light house is
A ladder 15 m long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then the height of the wall is
A man is standing on the deck of a ship, which is 40 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill `(sqrt(3) = 1.732)`
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole if the angle made by the rope with the ground level is 30°.
An observer 2.25 m tall is 42.75 m away from a chimney. The angle of elevation of the top of the chimney from her eyes is 45°. What is the height of the chimney?
