Advertisements
Advertisements
प्रश्न
A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass. [use π=22/7]
उत्तर
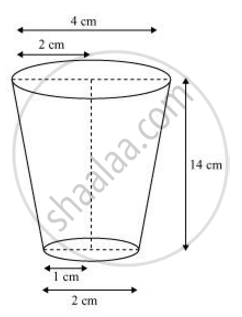
Radius (r1) of upper base of glass = 4/2 = 2 cm
Radius (r2) of lower base of glass = 2/2 = 1 cm
Capacity of glass = Volume of frustum of cone
`= 1/3pih = (r_1^2+r_2^2+r_1r_2)`
`=1/3pih[(2)^2 +(1)^2+(2)(1)]`
`=1/3xx22/7xx14[4+1+2]`
= 308/3 = 102 2/3 cm3
Therefore, the capacity of the glass is 102 2/3 cm3
संबंधित प्रश्न
Derive the formula for the curved surface area and total surface area of the frustum of cone.
A milk container of height 16 cm is made of metal sheet in the form of a frustum of a cone with radii of its lower and upper ends as 8 cm and 20 cm respectively . Find the cost of milk at the rate of ₹44 per litre which the container can hold.
An oil funnel of tin sheet consists of a cylindrical portion 10 cm long attached to a frustum of a cone. If the total height be 22 cm, the diameter of the cylindrical portion 8 cm and the diameter of the top of the funnel 18 cm, find the area of the tin required.(Use π = 22/7).
The radii of the circular ends of a solid frustum of a cone are 33 cm and 27 cm, and its slant height is 10 cm. Find its capacity and total surface area.
A right cylindrical vessel is full of water. How many right cones having the same radius and height as those of the right cylinder will be needed to store that water?
A bucket is in the form of a frustum of a cone with a capacity of 12308.8 cm3 of water. The radii of the top and bottom circular ends are
20 cm and 12 cm, respectively. Find the height of the bucket. [Use π = 3.14]
A milk container is made of metal sheet in the shape of frustum of a cone whose volume is `"10459" 3/7 "cm"`. The radii of its lower and upper circular ends are 8 cm and 20 cm, respectively. Find the cost of metal sheet used in making the container at the rate of ₹1.40 per cm2.
A cone is cut by a plane parallel to its base and the upper part is removed. The part that is left is called

The volume of the frustum of a cone is `1/3 pih[r_1^2 + r_2^2 - r_1r_2]`, where h is vertical height of the frustum and r1, r2 are the radii of the ends.
A milk container of height 16 cm is made of metal sheet in the form of a frustum of a cone with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk at the rate of Rs. 22 per litre which the container can hold.
