Advertisements
Advertisements
प्रश्न
An oil funnel of tin sheet consists of a cylindrical portion 10 cm long attached to a frustum of a cone. If the total height be 22 cm, the diameter of the cylindrical portion 8 cm and the diameter of the top of the funnel 18 cm, find the area of the tin required.(Use π = 22/7).
उत्तर
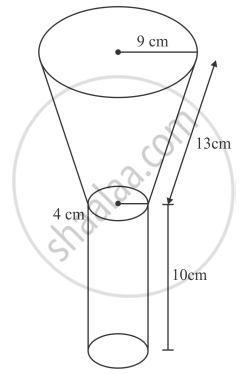
Let r1 and r2 (r1 > r2) be the radii of the ends of the frustum of a cone. Suppose l and hbe the slant height and height of frustum of cone.
Diameter of top of the frustum `2r_1 = 18 cm`
`r_1 = 9 cm`
Diameter of top of frustum `2r_2 = 8 cm`
`r_2 = 4 cm`
Let h1 be the height of the cylindrical portion.
Now, h1 = 10 cm
Total height of the funnel = 22 cm
height of frustum of cone, h = 22−10 = 12 cm
\[l = \sqrt{\left( r_1 - r_2 \right)^2 + h^2}\]
\[ \Rightarrow l = \sqrt{\left( 9 - 4 \right)^2 + \left( 12 \right)^2}\]
\[ \Rightarrow l = \sqrt{25 + 144}\]
\[ \Rightarrow l = \sqrt{169}\]
\[ \Rightarrow l = 13 cm\]
Curved surface area of funnel = CSA of frustum of cone + CSA of cylinder
Curved surface area of funnel = \[\pi\left( r_1 + r_2 \right)l + 2\pi r_2 h_1\]
Therefore,
Area of the tin required
\[= \pi\left( r_1 + r_2 \right)l + 2\pi r_2 h_1 \]
\[ = \pi\left[ \left( r_1 + r_2 \right)l + 2 r_2 h_1 \right]\]
\[ = \pi\left[ \left( 9 + 4 \right) \times 13 + 2 \times 4 \times 10 \right]\]
\[ = \pi\left[ 169 + 80 \right]\]
\[ = \pi\left[ 249 \right]\]
\[ = 249\pi {cm}^2\]
APPEARS IN
संबंधित प्रश्न
The slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm. find the curved surface area of the frustum.
A fez, the cap used by the Turks, is shaped like the frustum of a cone (see the figure given below). If its radius on the open side is 10 cm, radius at the upper base is 4 cm and its slant height is 15 cm, find the area of material use for making it. [use π=22/7]

Milk in a container, which is in the form of a frustum of a cone of height 30 cm and the radii of whose lower and upper circular ends are 20 cm and 40 cm respectively, is to be distributed in a camp for flood victims. If this milk is available at the rate of Rs 35 per litre and 880 litres of milk is needed daily for a camp, find how many such containers of milk are needed for a camp and what cost will it put on the donor agency for this. What value is indicated through this by the donor agency ?
The radii of the ends of a frustum are 14 cm and 6 cm respectively and its height is 6 cm. Find its curved surface area.
The radii of ends of a frustum are 14 cm and 6 cm respectively and its height is 6 cm. Find its volume \[\pi\] = 3.14)
A bucket is in the form of a frustum of a cone of height 30 cm with radii of its lower and upper ends as 10 cm and 20 cm respectively. Find the capacity and surface area of the bucket. Also, find the cost of milk which can completely fill the container , at thr rate of ₹25 per litre. (Use \[\pi = 3 . 14) .\]
A circus tent is cylindrical to a height of 3 metres and conical above it. If its diameter is 105 m and the slant height of the conical portion is 53 m, calculate the length of the canvas 5 m wide to make the required tent.
A cylinder and a cone are of the same base radius and of same height. Find the ratio of the value of the cylinder to that of the cone.
A container, open at the top and made up of metal sheet, is in the form of a frustum of a cone of height 16 cm with diameters of its lower and upper ends as 16 cm and 40 cm, respectively. Find the cost of metal sheet used to make the container, if it costs ₹10 per 100 cm2
A funnel is a combination of
