Advertisements
Advertisements
प्रश्न
A ladder of length 6meters makes an angle of 45° with the floor while leaning against one wall of a room. If the fort of the ladder is kept fixed on the floor and it is made to lean against the opposite wall of the room, it makes an angle of 60° with the floor. Find the
distance between two walls of the room.
उत्तर
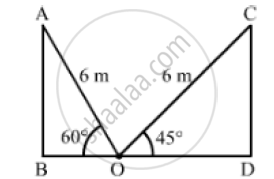
Let AB and CD be the two opposite walls of the room and the foot of the ladder be fixed at
the point O on the ground.
We have,
AO = CO = 6m,∠AOB = 60° and ∠COD = 45°
In ΔABO,
`cos 60°= (BD)/(AO)`
`⇒1/2 = (BO)/6`
`⇒ BO = 6/2`
⇒ BO = 3m
Also, in ΔCDO,
`cos 45° = (DO)/(CO)`
`⇒1/sqrt(2) = (DO)/6`
`⇒ DO = 6/sqrt(2) xx sqrt(2)/sqrt(2)`
`⇒DO = (6 sqrt(2))/2`
`⇒ Do = 3 sqrt(2) m`
Now, the distance between two walls of the room = BD
=BO+DO
`=3+3sqrt(2) `
`=3(1+sqrt(2))`
=3(1+1.414)
=3(2.414)
=7.242
`~~7.24m`
So, the distant between two walls of the room is 7. 24 m.
APPEARS IN
संबंधित प्रश्न
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
The angles of depression of the top and bottom of 8 m tall building from the top of a multistoried building are 30° and 45° respectively. Find the height of the multistoried building and the distance between the two buildings.
The angles of elevation of the top of a rock from the top and foot of a 100 m high tower are respectively 30° and 45°. Find the height of the rock.
A statue 1.46m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the status is 60 and from the same point, the angle of elevation of the top of the pedestal is 45 . Find the height of the pedestal.
A pole casts a shadow of length \[2\sqrt{3}\] m on the ground, when the sun's elevation is 60°. Find the height of the pole.
From the top of a lighthouse, an observer looking at a ship makes angle of depression of 60°. If the height of the lighthouse is 90 metre, then find how far the ship is from the lighthouse.
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with horizontal, then the length of the wire is
A tower is 60 m heigh. Its shadow is x metres shorter when the sun’s altitude is 45° than when it has been 30°, then x is equal to
From the top of a tower h m high, the angles of depression of two objects, which are in line with the foot of the tower are α and β (β > α). Find the distance between the two objects.
The angle of elevation of the top of a 30 m high tower at a point 30 m away from the base of the tower is ______.
