Advertisements
Advertisements
प्रश्न
The angles of depression of the top and bottom of 8 m tall building from the top of a multistoried building are 30° and 45° respectively. Find the height of the multistoried building and the distance between the two buildings.
उत्तर
Let AD be the multistoried building of height hm. And the angle of depression of the top and bottom are 30° and 45°. We assume that BE = 8, CD = 8 and BC = x, ED = x and AC = h − 8. Here we have to find height and distance of the building.
We use trigonometric ratio.
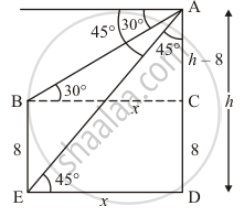
In ΔAED,
`=> tan E = (AD)/(DE)`
`=> tan 45^@= (AD)/(DE)`
`=> 1 = h/x`
=> x = h
Again in Δ ABC
`=> tan B = (AC)/(BC)`
`=> tan 30^@ = (h - 8)/x`
`=> 1/sqrt3 = (h - 8)/x`
`=> hsqrt3 - 8sqrt3 = x`
`> hsqrt3 - 8sqrt3 = h`
`=> h(sqrt3 - 1) = 8sqrt3`
`=> h = (8sqrt3)/(sqrt3 - 1) xx (sqrt3 + 1)/(sqrt3 + 1)`
`=> h = (24 + 8sqrt3)/2`
`=> h = (4(3 + sqrt3))`
And
`=> x = 4(3 + sqrt3)`
Hence the required height is `4(3 + sqrt3)` meter and distance is `4(3 + sqrt3)` meter
APPEARS IN
संबंधित प्रश्न
Two points A and B are on the same side of a tower and in the same straight line with its base. The angles of depression of these points from the top of the tower are 60° and 45° respectively. If the height of the tower is 15 m, then find the distance between the points.
An aeroplane is flying at a height of 300 m above the ground. Flying at this height, the angles of depression from the aeroplane of two points on both banks of a river in opposite directions are 45° and 60° respectively. Find the width of the river. [Use `sqrt3` = 1⋅732]
An observer, 1.5 m tall, is 28.5 m away from a tower 30 m high. Determine the angle of elevation of the top of the tower from his eye.
The angle of elevation of the top of a tower from ta point on the same level as the foot of the tower is 30° . On advancing 150 m towards foot of the tower, the angle of elevation becomes 60° Show that the height of the tower is 129.9 metres.
Two ships are approaching a light-house from opposite directions. The angles of depression of the two ships from the top of the light-house are 30° and 45°. If the distance between the two ships is 100 m, find the height of the light-house. \[[Use \sqrt{3} = 1 . 732]\]
A flag pole ‘h’ metres is on the top of the hemispherical dome of radius ‘r’ metres. A man is standing 7 m away from the dome. Seeing the top of the pole at an angle 45° and moving 5 m away from the dome and seeing the bottom of the pole at an angle 30°. Find radius of the dome `(sqrt(3) = 1.732)`
Two poles are 25 m and 15 m high, and the line joining their tops makes an angle of 45° with the horizontal. The distance between these poles is ______.
An observer 1.5 metres tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.
If a man standing on a platform 3 metres above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.
A person standing on the bank of a river observes that the angle of elevation of the top of a tree on the opposite bank of the river is 60° and when he retires 40 meters away from the tree the angle of elevation becomes 30°. The breadth of the river is ______.
