Advertisements
Advertisements
प्रश्न
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60° . At a point Y, 40m vertically above X, the angle of elevation is 45° . Find the height of tower PQ.
उत्तर
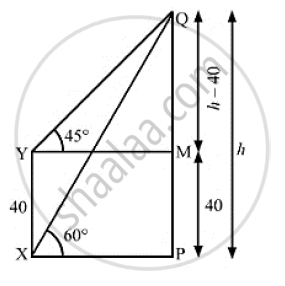
We have
XY = 40m,∠PXQ = 60° and ∠MYQ = 45°
Let PQ = h
Also, MP = XY = 40m, MQ = PQ - MP = h - 40
In ΔMYQ,
` tan 45° = (MQ)/(MY)`
`⇒1 = (h-40)/(MY)`
⇒ MY = H - 40
⇒ PX = MY = h - 40 ................(1)
Now , in ΔMXQ,
`tan 60° = (PQ)/(PX)`
`⇒ sqrt(3) = h/( h-40)` [From (i)]
`⇒ h sqrt(3) - 40 sqrt(3) = h `
`⇒ h sqrt(3) -h = 40 sqrt(3)`
`⇒ h (sqrt(3)-1) = 40 sqrt(3)`
`⇒ h = (40sqrt(3))/((sqrt(3)-1))`
`⇒ h = (40 sqrt(3))/((sqrt (3)-1)) xx ((sqrt(3)+1))/((sqrt(3)+1))`
`⇒ h = (40 sqrt(3)(sqrt(3)+1))/((3-1))`
`⇒h = (40 sqrt(3) ( sqrt(3) +1))/2`
`⇒h= 20sqrt(3) (sqrt(3)+1)`
`⇒ h= 60+20 sqrt(3)`
`⇒ h= 60+20xx 1.73`
`⇒h = 60+ 34.6`
∴ h = 94.6m
So, the height of the tower PQ is 94. 6 m.
APPEARS IN
संबंधित प्रश्न
The angle of elevation of an aeroplane from point A on the ground is 60˚. After flight of 15 seconds, the angle of elevation changes to 30˚. If the aeroplane is flying at a constant height of 1500√3 m, find the speed of the plane in km/hr.
The angle of elevation of the top of a tower from a point A on the ground is 30°. Moving a distance of 20metres towards the foot of the tower to a point B the angle of elevation increases to 60°. Find the height of the tower & the distance of the tower from the point A.
From the top of a 50 m high tower, the angles of depression of the top and bottom of a pole are observed to be 45° and 60° respectively. Find the height of the pole.
PQ is a post of given height a, and AB is a tower at some distance. If α and β are the angles of elevation of B, the top of the tower, at P and Q respectively. Find the height of the tower and its distance from the post.
An observer, 1.7 m tall, is 203–√203 m away from a tower. The angle of elevation from the of observer to the top of tower is 30°. Find the height of tower ?
A solid right-circular cone of height 60 cm and radius 30 cm is dropped in a right-circular cylinder full of water of height 180 cm and radius 60 cm. Find the volume of water left in the cylinder, in cubic metres ?
From a light house the angles of depression of two ships on opposite sides of the light house are observed to be 30° and 45°. If the height of the light house is h metres, the distance between the ships is
A ladder makes an angle of 60º with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder (in metres) is
If two circles having centers P and Q and radii 3 cm and 5 cm. touch each other externally, find the distance PQ.
The angle of elevation of the top of a vertical tower from a point A, due east of it is 45°. The angle of elevation of the top of the same tower from a point B, due south of A is 30°. If the distance between A and B is `54sqrt(2)` m, then the height of the tower (in metres), is ______.
