Advertisements
Advertisements
Question
Read the following passage and answer the questions given below.
|
A 'circus' is a company of performers who put on shows of acrobats, clowns etc. to entertain people started around 250 years back, in open fields, now generally performed in tents. One such 'Circus Tent' is shown below. The tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of cylindrical part are 9 m and 30 m respectively and height of conical part is 8 m with same diameter as that of the cylindrical part, then find |
- the area of the canvas used in making the tent;
- the cost of the canvas bought for the tent at the rate ₹ 200 per sq m, if 30 sq m canvas was wasted during stitching.
Solution
According to given information, we have the following figure.
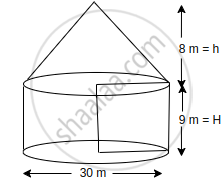
Clearly, the radius of conical part = radius of cylindrical part = `30/2` = 15 m = r ...(say)
Let h and H be the height of conical and cylindrical part respectively.
Then h = 8 m and H = 9 m
∴ l = `sqrt(r^2 + h^2)`
= `sqrt((15)^2 + 8^2)`
= `sqrt(225 + 64)`
= `sqrt(289)`
= 17 m
1. The area of the canvas used in making the tent
= Curved surface area of cone + Curved surface area of cylinder
= πrl + 2πrH
= πr(l + 2H)
= `22/7 xx 15(17 + 2 xx 9)`
= `22/7 xx 15 xx 35`
= 1650 m2
2. Area of canvas bought for the tent
= (1650 + 30) m2
= 1680 m2
Now, this cost of the canvas height for the tent
= ₹ (1680 × 200)
= ₹ 3,36,000
APPEARS IN
RELATED QUESTIONS
A metallic solid sphere of radius 10.5 cm is melted and recasted into smaller solid cones, each of radius 3.5 cm and height 3 cm. How many cones will be made?
A 5 m wide cloth is used to make a conical tent of base diameter 14 m and height 24 m. Find the cost of cloth used at the rate of Rs 25 per metre ?\[[Use \pi = \frac{22}{7}]\]
The surface area of a sphere is the same as the curved surface area of a cone having the radius of the base as 120 cm and height 160 cm. Find the radius of the sphere.
A bucket is in the form of a frustum of a cone and holds 15.25 litres of water. The diameters of the top and bottom are 25 cm and 20 cm respectively. Find its height and area of tin used in its construction.
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. What is the ratio of their volumes?
If the slant height of the frustum of a cone is 6 cm and the perimeters of its circular bases are 24 cm and 12 cm respectively. What is the curved surface area of the frustum?
A metallic sphere of radius 10.5 cm is melted and then recast into small cones, each of radius 3.5 cm and height 3 cm. The number of such cones is
A hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. The height of the cone is
A bucket made up of a metal sheet is in the form of a frustum of a cone of height 16 cm and radii of its lower and upper ends are 8 cm and 20 cm, respectively. Find the cost of the bucket if the cost of metal sheet used is Rs 15 per 100 cm2.
An open metal bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet. The diameters of the two circular ends of the bucket are 45 cm and 25 cm, the total vertical height of the bucket is 40 cm and that of the cylindrical base is 6 cm. Find the area of the metallic sheet used to make the bucket. Also, find the volume of water the bucket can hold, in litres.

