Advertisements
Advertisements
Question
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. What is the ratio of their volumes?
Solution
Let r be the radius of the base.
And h is the height.
Here, h = r.
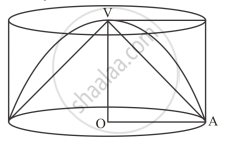
Now,
The ratio of their volumes will be
Volume of cone: volume of hemisphere: volume of a cylinder
`1/3pir^2 h : 2/3pir^3 : pir^2 h `
`V_1 :V_2 :V_3 = 1/3pir^3 : 2/3 pir^3 : pir^3`
Hence , `V_1 : V_2 :V_3 = 1:2:3`
APPEARS IN
RELATED QUESTIONS
A bucket, made of metal sheet, is in the form of a cone whose height is 35 cm and radii of circular ends are 30 cm and 12 cm. How many litres of milk it contains if it is full to the brim? If the milk is sold at Rs 40 per litre, find the amount received by the person.
A frustum of a cone is 9 cm thick and the diameters of its circular ends are 28 cm and 4 cm. Find the volume and lateral surface area of the frustum.
(Take π = 22/7).
If a cone and a sphere have equal radii and equal volumes. What is the ratio of the diameter of the sphere to the height of the cone?
A container in the shape of a frustum of a cone having diameters of its two circular faces as 35 cm and 30 cm and vertical height 14 cm,
is completely filled with oil. If each cm3 of oil has mass 1.2 g, then find the cost of oil in the container if it costs ₹40 per kg.
A bucket is in the form of a frustum of a cone and it can hold 28.49 litres of water. If the radii of its circular ends are 28 cm and 21 cm, then find the height of the bucket.
A tent consists of a frustum of a cone, surmounted by a cone. If the diameter of the upper and lower circular ends of the frustum be 14 m and 26 m, respectively, the height of the frustum be 8 m and the slant height of the surmounted conical portion be 12 m, find the area of the canvas required to make the tent. (Assume that the radii of the upper circular end of the frustum and the base of the surmounted conical portion are equal.)
A cone is cut by a plane parallel to its base and the upper part is removed. The part that is left is called

The radii of the top and bottom of a bucket of slant height 13 cm are 9 cm and 4 cm respectively. The height of the bucket is ______.
The volume of the frustum of a cone is `1/3 pih[r_1^2 + r_2^2 - r_1r_2]`, where h is vertical height of the frustum and r1, r2 are the radii of the ends.
An open metallic bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet. The surface area of the metallic sheet used is equal to curved surface area of frustum of a cone + area of circular base + curved surface area of cylinder.
