Advertisements
Advertisements
Question
A hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. The height of the cone is
Options
12 cm
14 cm
15 cm
18 cm
Solution
External radius `r_1 = 8/2 = 4 cm`
Internal radius `r_2 = 4/2 = 2cm`
The volume of hollow sphere
\[V = \frac{4}{3}\pi\left( R^3 - r^3 \right)\]
\[ = \frac{4}{3}\pi\left( 4^3 - 2^3 \right)\]
Let h be the height of cone.
Clearly,
The volume of recasted cone = volume of hollow sphere
\[\frac{1}{3} \pi r^2 h = \frac{4}{3}\pi\left( 4^3 - 2^3 \right)\]
\[ \Rightarrow 4^2 h = 4\left( 4^3 - 2^3 \right)\]
\[ \Rightarrow h = 14 cm\]
Hence, the height of cone = 14 cm
APPEARS IN
RELATED QUESTIONS
A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass. [use π=22/7]
A bucket is in the form of a frustum of a cone of height 30 cm with radii of its lower and upper ends as 10 cm and 20 cm respectively. Find the capacity and surface area of the bucket. Also, find the cost of milk which can completely fill the container , at thr rate of ₹25 per litre. (Use \[\pi = 3 . 14) .\]
A right circular cone and a right circular cylinder have equal base and equal height. If the radius of the base and height are in the ratio 5 : 12, write the ratio of the total surface area of the cylinder to that of the cone.
If r1 and r2 denote the radii of the circular bases of the frustum of a cone such that r1 > r2, then write the ratio of the height of the cone of which the frustum is a part to the height fo the frustum.
A hemisphere of lead of radius 9 cm is cast into a right circular cone of height 72 cm. Find the radius of the base of the cone.
A container in the shape of a frustum of a cone having diameters of its two circular faces as 35 cm and 30 cm and vertical height 14 cm,
is completely filled with oil. If each cm3 of oil has mass 1.2 g, then find the cost of oil in the container if it costs ₹40 per kg.
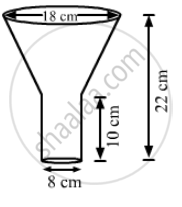
An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, then find the area of the tin sheet required to make the funnel.
A bucket of height 24 cm is in the form of frustum of a cone whose circular ends are of diameter 28 cm and 42 cm. Find the cost of milk at the rate of ₹30 per litre, which the bucket can hold.
An oil funnel of the tin sheet consists of a cylindrical portion 10 cm long attached to a frustum of a cone. If the total height is 22 cm, the diameter of the cylindrical portion by 8 cm and the diameter of the top of the funnel be 18 cm, then find the area of the tin sheet required to make the funnel.
Find the total surface area of frustum, if its radii are 15 cm and 7 cm. Also, the slant height of the frustum is 14 cm.
Radii of the frustum = `square` cm and `square` cm
Slant height of the frustum = `square` cm
Total surface area = `π[(r_1^2 + r_2^2 + (r_1 + r_2)l]`
= `22/7 [square + square + (square + square) square]`
= `22/7 (square)`
= `square` cm2
Hence, the total surface area of the frustum is `square`.
