Advertisements
Advertisements
Question
If r1 and r2 denote the radii of the circular bases of the frustum of a cone such that r1 > r2, then write the ratio of the height of the cone of which the frustum is a part to the height fo the frustum.
Solution
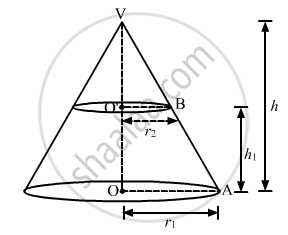
Since, `Delta VO'B - DeltaVOA `
Therefore,
In `Delta VO'B - DeltaVOA `
`(O'B)/(OA) = (O'V)/(OV)`
`r_2/r_1 = (h -h_1)/(h)`
`r_2/r_2 = 1 - h_1/h`
`h_1/h = 1 - r_2/r_1`
`= (r_1 - r_2)/r_1`
Hence,
The ratio of the height of cone of which the frustum is a part to the height fo the frustum.
\[\frac{OV}{OO'} = \frac{h}{h_1} = \frac{r_1}{r_1 - r_2}\]
Hence, `h : h_1 = r_1 :(r_1 - r_2)`
APPEARS IN
RELATED QUESTIONS
A fez, the cap used by the Turks, is shaped like the frustum of a cone (see the figure given below). If its radius on the open side is 10 cm, radius at the upper base is 4 cm and its slant height is 15 cm, find the area of material use for making it. [use π=22/7]

The radii of ends of a frustum are 14 cm and 6 cm respectively and its height is 6 cm. Find its volume \[\pi\] = 3.14)
An oil funnel of tin sheet consists of a cylindrical portion 10 cm long attached to a frustum of a cone. If the total height be 22 cm, the diameter of the cylindrical portion 8 cm and the diameter of the top of the funnel 18 cm, find the area of the tin required.(Use π = 22/7).
The radii of the circular ends of a solid frustum of a cone are 18 cm and 12 cm and its height is 8 cm. Find its total surface area. [Use π = 3.14]
A solid metallic right circular cone 20 cm high and whose vertical angle is 60°, is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter `1/12` cm, then find the length of the wire.
A bucket is in the form of a frustum of a cone with a capacity of 12308.8 cm3 of water. The radii of the top and bottom circular ends are
20 cm and 12 cm, respectively. Find the height of the bucket. [Use π = 3.14]
Choose the correct answer of the following question:
If the height of a bucket in the shape of frustum of a cone is 16 cm and the diameters of its two circular ends are 40 cm and 16 cm, then its slant height is
A frustum of a right circular cone is of height 16 cm with radius of its ends as 8 cm and 20 cm. Then, the volume of the frustum is
An oil funnel of the tin sheet consists of a cylindrical portion 10 cm long attached to a frustum of a cone. If the total height is 22 cm, the diameter of the cylindrical portion by 8 cm and the diameter of the top of the funnel be 18 cm, then find the area of the tin sheet required to make the funnel.
Find the curved surface area of a right circular cone whose height is 15 cm and base radius is 8 cm. tan β = `3/4`.
