Advertisements
Advertisements
प्रश्न
If r1 and r2 denote the radii of the circular bases of the frustum of a cone such that r1 > r2, then write the ratio of the height of the cone of which the frustum is a part to the height fo the frustum.
उत्तर
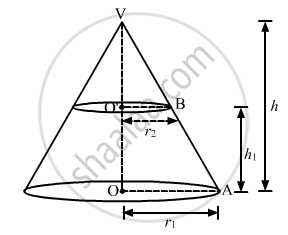
Since, `Delta VO'B - DeltaVOA `
Therefore,
In `Delta VO'B - DeltaVOA `
`(O'B)/(OA) = (O'V)/(OV)`
`r_2/r_1 = (h -h_1)/(h)`
`r_2/r_2 = 1 - h_1/h`
`h_1/h = 1 - r_2/r_1`
`= (r_1 - r_2)/r_1`
Hence,
The ratio of the height of cone of which the frustum is a part to the height fo the frustum.
\[\frac{OV}{OO'} = \frac{h}{h_1} = \frac{r_1}{r_1 - r_2}\]
Hence, `h : h_1 = r_1 :(r_1 - r_2)`
APPEARS IN
संबंधित प्रश्न
A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass. [use π=22/7]
Derive the formula for the volume of the frustum of a cone.
A solid toy s in the form of a hemisphere surrounded by a right circular cone . The height of cone is 4 cm and the diameter of the base is 8 cm . Determine the volume of the toy. If a cube circumscribes the toy , then find the difference of the volumes of cube and the toy .
The surface area of a sphere is the same as the curved surface area of a cone having the radius of the base as 120 cm and height 160 cm. Find the radius of the sphere.
The radii of the circular ends of a frustum are 6 cm and 14 cm. If its slant height is 10 cm, then its vertical height is
A bucket made up of a metal sheet is in the form of a frustum of a cone of height 16 cm and radii of its lower and upper ends are 8 cm and 20 cm, respectively. Find the cost of the bucket if the cost of metal sheet used is Rs 15 per 100 cm2.
Choose the correct answer of the following question:
If the height of a bucket in the shape of frustum of a cone is 16 cm and the diameters of its two circular ends are 40 cm and 16 cm, then its slant height is
The slant height of a frustum of a cone is 4 m and the perimeter of circular ends is 18 m and 16 m. Find the cost of painting its curved surface area at ₹ 100 per sq. m
Find the total surface area of frustum, if its radii are 15 cm and 7 cm. Also, the slant height of the frustum is 14 cm.
Radii of the frustum = `square` cm and `square` cm
Slant height of the frustum = `square` cm
Total surface area = `π[(r_1^2 + r_2^2 + (r_1 + r_2)l]`
= `22/7 [square + square + (square + square) square]`
= `22/7 (square)`
= `square` cm2
Hence, the total surface area of the frustum is `square`.
