Advertisements
Advertisements
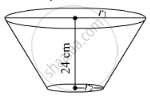
प्रश्न
उत्तर
Radius of one circular end, r1 = 14 cm
Radius of other circular end, r2 = 7 cm
Height of the bucket, h = 30 cm
∴ Volume of water in the bucket = Volume of frustum of cone
\[= \frac{1}{3}\pi h\left( r_1^2 + r_1 r_2 + r_2^2 \right)\]
\[ = \frac{1}{3} \times \frac{22}{7} \times 30 \times \left( {14}^2 + 14 \times 7 + 7^2 \right)\]
\[ = \frac{1}{3} \times \frac{22}{7} \times 30 \times 343\]
\[ = 10780 {cm}^3\]
\[= \frac{10780}{1000}\] ...[∵ 1 litre = 1000cm3]
= 10.78 L
Thus, the bucket can hold 10.78 litres of water.
APPEARS IN
संबंधित प्रश्न
A container, opened from the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of the milk which can completely fill the container, at the rate of Rs.20 per litre. Also find the cost of metal sheet used to make the container, if it costs Rs.8 per 100 cm2. [Take π = 3.14]
Derive the formula for the curved surface area and total surface area of the frustum of cone.
A 5 m wide cloth is used to make a conical tent of base diameter 14 m and height 24 m. Find the cost of cloth used at the rate of Rs 25 per metre ?\[[Use \pi = \frac{22}{7}]\]
The circumferences of circular faces of a frustum are 132 cm and 88 cm and its height is 24 cm. To find the curved surface area of the frustum complete the following activity.( \[\pi = \frac{22}{7}\])
A solid metallic sphere of radius 10.5 cm is melted and recast into a number of smaller cones, each of radius 3.5 cm and height 3 cm. Find the number of cones so formed.
A solid right circular cone of height 120 cm and radius 60 cm is placed in a right circular cylinder full of water of height 180 cm such that it touches the bottom . Find the volume of water left in the cylinder , if the radius of the cylinder is equal to the radius of te cone
A milk container of height 16 cm is made of metal sheet in the form of a frustum of a cone with radii of its lower and upper ends as 8 cm and 20 cm respectively . Find the cost of milk at the rate of ₹44 per litre which the container can hold.
A circus tent is cylindrical to a height of 3 metres and conical above it. If its diameter is 105 m and the slant height of the conical portion is 53 m, calculate the length of the canvas 5 m wide to make the required tent.
The material of a cone is converted into the shape of a cylinder of equal radius. If height of the cylinder is 5 cm, then height of the cone is
The height and radius of the cone of which the frustum is a part are h1 and r1 respectively. If h2 and r2 are the heights and radius of the smaller base of the frustum respectively and h2 : h1 = 1 : 2, then r2 : r1 is equal to
A container in the shape of a frustum of a cone having diameters of its two circular faces as 35 cm and 30 cm and vertical height 14 cm,
is completely filled with oil. If each cm3 of oil has mass 1.2 g, then find the cost of oil in the container if it costs ₹40 per kg.
A solid metallic right circular cone 20 cm high and whose vertical angle is 60°, is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter `1/12` cm, then find the length of the wire.
The radii of the circular ends of a frustum of height 6 cm are 14 cm and 6 cm, respectively. Find the slant height of the frustum.
A solid metallic sphere of diameter 28 cm is melted and recast into a number of smaller cones, each of diameter `"4"2/3` cm and height 3 cm. Find the number of cones so formed.
A funnel is a combination of
A cone is cut by a plane parallel to its base and the upper part is removed. The part that is left is called

By melting a solid sphere of radius 5 cm a solid right circular cone of the same circular base radius is made. The height of cone is ______.
A cone is cut through a plane parallel to its base and then the cone that is formed on one side of that plane is removed. The new part that is left over on the other side of the plane is called ______.
A metallic spherical shell of internal and external diameters 4 cm and 8 cm, respectively is melted and recast into the form a cone of base diameter 8 cm. The height of the cone is ______.
