Advertisements
Advertisements
प्रश्न
A container, opened from the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of the milk which can completely fill the container, at the rate of Rs.20 per litre. Also find the cost of metal sheet used to make the container, if it costs Rs.8 per 100 cm2. [Take π = 3.14]
उत्तर
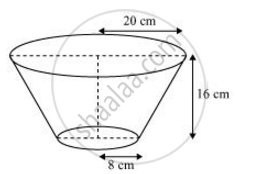
Radius (r1) of upper end of container = 20 cm
Radius (r2) of lower end of container = 8 cm
Height (h) of container = 16 cm
Slant height (l) of frustum = `sqrt((r_1-r_2)^2+h^2)`
`=sqrt((20-8)^2+(16)^2)`
`=sqrt((12)^2+(16)^2) = sqrt(144+256)`
= 20 cm
Capacity of container = Volume of frustum
`=1/3pih(r_1^2+r_2^2+r_1r_2)`
`=1/3xx3.14xx16xx[(20)^2+(8)^2+(20)(8)]`
`=1/3xx3.14xx16(400+64+160)`
`=1/3xx3.14xx16xx624`
= 10449.92 cm3
= 10.45 litres.
Cost of 1 litre milk = Rs 20
Cost of 10.45 litre milk = 10.45 × 20
= Rs 209
Area of metal sheet used to make the container
`=pi(r_1+r_2)l + pir_2^2`
= π (20 + 8) 20 + π (8)2
= 560 π + 64 π = 624 π cm2
Cost of 100 cm2 metal sheet = Rs 8
Cost of 624 π cm2 metal sheet = `(624 xx 3.14 xx 8)/100`
= 156.75
Therefore, the cost of the milk which can completely fill the container is
Rs 209 and the cost of metal sheet used to make the container is Rs 156.75.
APPEARS IN
संबंधित प्रश्न
A bucket is in the form of a frustum of a cone of height 30 cm with radii of its lower and upper ends as 10 cm and 20 cm respectively. Find the capacity and surface area of the bucket. Also, find the cost of milk which can completely fill the container , at thr rate of ₹25 per litre. (Use \[\pi = 3 . 14) .\]
The surface area of a sphere is the same as the curved surface area of a cone having the radius of the base as 120 cm and height 160 cm. Find the radius of the sphere.
A cone of radius 4 cm is divided into two parts by drawing a plane through the mid point of its axis and parallel to its base . Compare the volumes of two parts.
The radii of the base of a cylinder and a cone are in the ratio 3 : 4 and their heights are in the ratio 2 : 3. What is the ratio of their volumes?
The curved surface area of a right circular cone of height 15 cm and base diameter 16 cm is
A cone of height 20 cm and radius of base 5 cm is made up of modelling clay. A child reshapes it in the form of a sphere. Find the diameter of the sphere.
A metallic bucket, open at the top, of height 24 cm is in the form of the frustum of a cone, the radii of whose lower and upper circular ends are 7 cm and 14 cm, respectively. Find
- the volume of water which can completely fill the bucket;
- the area of the metal sheet used to make the bucket.
The radii of the circular ends of a solid frustum of a cone are 33 cm and 27 cm and its slant height is 10 cm. Find its total surface area. [Use π = 3.14.]
The diameters of two circular ends of a bucket are 44 cm and 24 cm, and the height of the bucket is 35 cm. The capacity of the bucket is
The number of conical bottles of radius 2 cm and height 3.6 cm, required to empty the liquid from a cylindrical bottle of radius 6 cm and height 10 cm is ______.
