Advertisements
Advertisements
प्रश्न
A metallic spherical shell of internal and external diameters 4 cm and 8 cm, respectively is melted and recast into the form a cone of base diameter 8 cm. The height of the cone is ______.
विकल्प
12 cm
14 cm
15 cm
18 cm
उत्तर
A metallic spherical shell of internal and external diameters 4 cm and 8 cm, respectively is melted and recast into the form a cone of base diameter 8cm. The height of the cone is 14 cm.
Explanation: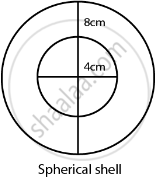
Volume of spherical shell = Volume of cone recast by melting
For spherical shell,
Internal diameter, d1 = 4 cm
Internal radius, r1 = 2 cm ...[As radius = `1/2` diameter]
External diameter, d2 = 8 cm
External radius, r2 = 4 cm
Now,
As volume of spherical shell= `4/3 π("r"_2^3 - "r"_1^3)`
Where r1 and r2 are internal and external radii respectively.
Volume of given shell = `4/3 π(4^3 - 2^3)`
= `4/3 π(56)`
= `(224/3)π`
We know that,
Volume of cone = `(224π)/3 "cm"^3`
For cone,
Base diameter = 8 cm
Base radius, r = 4 cm
Let Height of cone = ‘h’.
We know,
Volume of cone = `(1/3)π "r"^2"h"`,
Where r = Base radius and h = Height of cone
Volume of given cone = `(1/3)π4^2"h"`
⇒ `(224π)/3 = (16π"h")/3`
⇒ 16h = 224
h = 14 cm
So, Height of cone is 14 cm.
APPEARS IN
संबंधित प्रश्न
Derive the formula for the volume of the frustum of a cone.
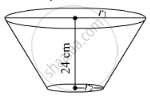
The circumferences of circular faces of a frustum are 132 cm and 88 cm and its height is 24 cm. To find the curved surface area of the frustum complete the following activity.( \[\pi = \frac{22}{7}\])
The radii of the circular ends of a solid frustum of a cone are 33 cm and 27 cm and its slant height is 10 cm. Find its total surface area.
A hemisphere of lead of radius 7 cm is cast into a right circular cone of height 49 cm. Find the radius of the base.
In a right circular cone , the cross-section made by a plane parallel to the base is a
The radii of the circular ends of a solid frustum of a cone are 33 cm and 27 cm and its slant height is 10 cm. Find its total surface area. [Use π = 3.14.]
The radii of the circular ends of a frustum of height 6 cm are 14 cm and 6 cm, respectively. Find the slant height of the frustum.
Find the total surface area of frustum, if its radii are 15 cm and 7 cm. Also, the slant height of the frustum is 14 cm.
Radii of the frustum = `square` cm and `square` cm
Slant height of the frustum = `square` cm
Total surface area = `π[(r_1^2 + r_2^2 + (r_1 + r_2)l]`
= `22/7 [square + square + (square + square) square]`
= `22/7 (square)`
= `square` cm2
Hence, the total surface area of the frustum is `square`.
Find the curved surface area of a right circular cone whose height is 15 cm and base radius is 8 cm. tan β = `3/4`.
If radius of the base of cone is 7 cm and height is 24 cm, then find its slant height.
