Advertisements
Advertisements
प्रश्न
Derive the formula for the volume of the frustum of a cone.
उत्तर
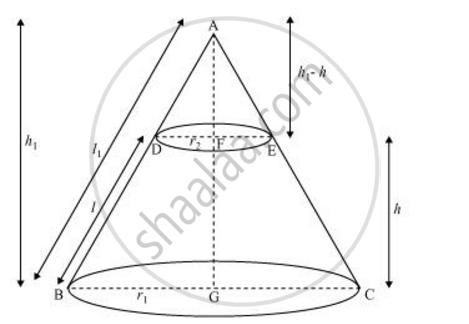
Let ABC be a cone. A frustum DECB is cut by a plane parallel to its base.
Let r1 and r2 be the radii of the ends of the frustum of the cone and h be the height of the frustum of the cone.
In ΔABG and ΔADF, DF||BG
∴ ΔABG ∼ ΔADF
DF/BG = AF/AG = AD/AB
`r_2/r_1 = (h_1-h)/h_1 = (l_1-l)/l_1`
`r_2/r_1 =1 -h/h_1 =1 -l/l_1`
`1-h/h_1= r_2/r_1`
`h/h_1 =1 -r_2/r_1 = (r_1-r_2)/r_1`
`h_1/h= r_1/(r_1-r_2)`
`h_1 = (r_1h)/(r_1-r_2)`
Volume of frustum of cone = Volume of cone ABC − Volume of cone ADE
`=1/3pir_1^2h_1 - 1/3pir_2^2(h_1-h)`
`=pi/3[r_1^2h_1-r_2^2(h_1-h)]`
`=pi/3[r_1^2((hr_1)/(r_1-r_2))-r_2^2((hr_1)/(r_1-r_2)-h)]`
`=pi/3[((hr_1^3)/(r_1-r_2))-r_2^2((hr_1-hr_1+hr_2)/(r_1-r_2))]`
`=pi/3[(hr_1^3)/(r_1-r_2)-(hr_2^3)/(r_1-r_2)]`
`=pi/3h[(r_1^3-r_2^3)/(r_1-r_2)]`
`=pi/3h[((r_1-r_2)(r_1^2+r_2^2+r_1r_2))/(r_1-r_2)]`
`= 1/3pih[r_1^2+r_2^2+r_1r_2]`
APPEARS IN
संबंधित प्रश्न
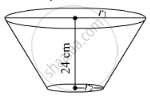
A metallic bucket, open at the top, of height 24 cm is in the form of the frustum of a cone, the radii of whose lower and upper circular ends are 7 cm and 14 cm respectively. Find :
(i) the volume of water which can completely fill the bucket.
(ii) the area of the metal sheet used to make the bucket.
[Use π =\[\frac{22}{7}\]
The circumferences of circular faces of a frustum are 132 cm and 88 cm and its height is 24 cm. To find the curved surface area of the frustum complete the following activity.( \[\pi = \frac{22}{7}\])
A cone of height 20 cm and radius of base 5 cm is made up of modeling clay. A child reshapes it in the form of a sphere. Find the diameter of the sphere.
A solid toy s in the form of a hemisphere surrounded by a right circular cone . The height of cone is 4 cm and the diameter of the base is 8 cm . Determine the volume of the toy. If a cube circumscribes the toy , then find the difference of the volumes of cube and the toy .
The height and radius of the cone of which the frustum is a part are h1 and r1 respectively. If h2 and r2 are the heights and radius of the smaller base of the frustum respectively and h2 : h1 = 1 : 2, then r2 : r1 is equal to
A frustum of a right circular cone is of height 16 cm with radius of its ends as 8 cm and 20 cm. Then, the volume of the frustum is
A cone is cut through a plane parallel to its base and then the cone that is formed on one side of that plane is removed. The new part that is left over on the other side of the plane is called ______.
A metallic spherical shell of internal and external diameters 4 cm and 8 cm, respectively is melted and recast into the form a cone of base diameter 8 cm. The height of the cone is ______.
A milk container of height 16 cm is made of metal sheet in the form of frustum of a cone with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk at the rate of ₹ 22 per litre which the container can hold.
