Advertisements
Advertisements
प्रश्न
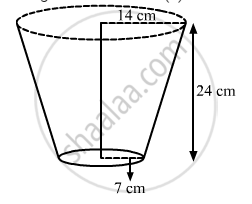
A metallic bucket, open at the top, of height 24 cm is in the form of the frustum of a cone, the radii of whose lower and upper circular ends are 7 cm and 14 cm respectively. Find :
(i) the volume of water which can completely fill the bucket.
(ii) the area of the metal sheet used to make the bucket.
[Use π =\[\frac{22}{7}\]
उत्तर
Upper radius of the bucket (R) = 14 cm
Lower radius of the bucket (r) = 7 cm
Height of the bucket (h) = 24 cm
Slant height of the bucket (l) =\[\sqrt{h^2 + (R - r )^2}\]
\[\Rightarrow V = \left\{ \frac{1}{3}\pi\left( {14}^2 + 14 \times 7 + 7^2 \right) \right\}24 {cm}^3 \]
\[ = \left( \frac{1}{3} \times \frac{22}{7} \times 343 \times 24 \right) {cm}^3 \]
\[ = 8624 {cm}^3\]
Thus, the volume of water that can completely fill the bucket is 8624 cm3.
(ii) To measure the area of the metal sheet used in making the bucket, we need to find the surface area of the bucket.
Surface area of the bucket = Curved surface area of the frustum + Curved surface area of the circular base
=\[\pi\left( R + r \right)l + \pi r^2\]
=\[\left( \frac{22}{7} \times \left( 14 + 7 \right) \times 25 + \frac{22}{7} \times 7^2 \right) {cm}^2\]
= \[\left( 1650 + 154 \right) {cm}^2\]
=\[1804 {cm}^2\]
APPEARS IN
संबंधित प्रश्न
A metallic right circular cone 20 cm high and whose vertical angle is 60° is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained is drawn into a wire of diameter 1/16 cm, find the length of the wire [use π=22/7]
The radii of the ends of a frustum of a right circular cone are 5 metres and 8 metres and its lateral height is 5 metres. Find the lateral surface and volume of the frustum.
A right circular cone and a right circular cylinder have equal base and equal height. If the radius of the base and height are in the ratio 5 : 12, write the ratio of the total surface area of the cylinder to that of the cone.
A right triangle with sides 3 cm, 4 cm and 5 cm is rotated about the side of 3 cm to form a cone. The volume of the cone so formed is
A metalic solid cone is melted to form a solid cylinder of equal radius. If the height of the cylinder is 6 cm, then the height of the cone was
The height of a right circular cone is 20 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume be `1/8` of the volume of the given cone, then at what height above the base is the section made?
A frustum of a right circular cone is of height 16 cm with radius of its ends as 8 cm and 20 cm. Then, the volume of the frustum is
An oil funnel of the tin sheet consists of a cylindrical portion 10 cm long attached to a frustum of a cone. If the total height is 22 cm, the diameter of the cylindrical portion by 8 cm and the diameter of the top of the funnel be 18 cm, then find the area of the tin sheet required to make the funnel.
In a right circular cone, the cross-section made by a plane parallel to the base is a ______.
Read the following passage and answer the questions given below.
|
A 'circus' is a company of performers who put on shows of acrobats, clowns etc. to entertain people started around 250 years back, in open fields, now generally performed in tents. One such 'Circus Tent' is shown below. The tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of cylindrical part are 9 m and 30 m respectively and height of conical part is 8 m with same diameter as that of the cylindrical part, then find |
- the area of the canvas used in making the tent;
- the cost of the canvas bought for the tent at the rate ₹ 200 per sq m, if 30 sq m canvas was wasted during stitching.

