Advertisements
Advertisements
प्रश्न
If the slant height of the frustum of a cone is 6 cm and the perimeters of its circular bases are 24 cm and 12 cm respectively. What is the curved surface area of the frustum?
उत्तर
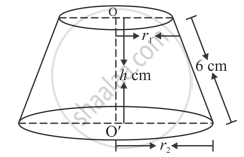
The parameter of upper base
`=2pir_1`
`2pir_1= 12`
`r_1 = 6/pi cm`
The parameter of lower base
`=2pir_2`
`2pir_2= 24`
`r_2 = 12/pi cm`
The surface area of frustum
`=pi(6/pi + 12/pi) xx 6`
`= pi xx 18/pi xx 6`
`=108 cm^2`
APPEARS IN
संबंधित प्रश्न
A metal container, open from the top, is in the shape of a frustum of a cone of height 21 cm with radii of its lower and upper circular ends as 8 cm and 20 cm respectively. Find the cost of milk which can completely fill the container at the rate of Rs 35 per litre.\[\left[ Use \pi = \frac{22}{7} \right]\]
The circumferences of circular faces of a frustum are 132 cm and 88 cm and its height is 24 cm. To find the curved surface area of the frustum complete the following activity.( \[\pi = \frac{22}{7}\])
A metallic hemisphere is melted and recast in the shape of a cone with the same base radius R as that of the hemisphere. If H is the height of the cone, then write the values of \[\frac{H}{R} .\]
A solid consists of a circular cylinder with an exact fitting right circular cone placed at the top. The height of the cone is h. If the total volume of the solid is 3 times the volume of the cone, then the height of the circular is
The height and radius of the cone of which the frustum is a part are h1 and r1 respectively. If h2 and r2 are the heights and radius of the smaller base of the frustum respectively and h2 : h1 = 1 : 2, then r2 : r1 is equal to
A milk container is made of metal sheet in the shape of frustum of a cone whose volume is `"10459" 3/7 "cm"`. The radii of its lower and upper circular ends are 8 cm and 20 cm, respectively. Find the cost of metal sheet used in making the container at the rate of ₹1.40 per cm2.
A drinking glass is in the shape of the frustum of a cone of height 21 cm with 6 cm and 4 cm as the diameters of its two circular ends. Find the capacity of the glass.
The slant height of the frustum of a cone having radii of two ends as 5 cm and 2 cm respectively and height 4 cm is ______.
The volume of the frustum of a cone is `1/3 pih[r_1^2 + r_2^2 - r_1r_2]`, where h is vertical height of the frustum and r1, r2 are the radii of the ends.
If radius of the base of cone is 7 cm and height is 24 cm, then find its slant height.
