Advertisements
Advertisements
Question
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. From a point Y, 40 m vertically above X, the angle of elevation of the top Q of tower is 45. Find the height of the tower PQ and the distance PX. (Use `sqrt3=1.73)`
Solution
MP = YX = 40 m
∴ QM = h - 40
In right angled ΔQMY,
`tan45^@=(QM)/(MY)=>1=(h-40)/(PX) " ...."(MY=PX)`
∴ PX = h - 40 ....(1)
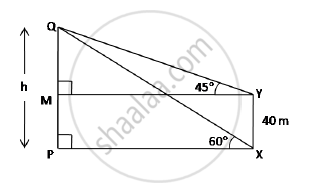
In right angled ΔQPX,
`tan60^@=(QP)/(PX)=>sqrt3=(QP)/(PX)`
∴ `PX=h/sqrt3 " ...(2)"`
From (1) and (2), h - 40 = `h/sqrt3`
`:.sqrt(3h)-40sqrt3=h`
`:.sqrt(3h)-h=40sqrt3`
∴ 1.73h - h=40(1.73) ⇒ h = 94.79 m
Thus, PQ is 94.79 m.
APPEARS IN
RELATED QUESTIONS
An electric pole is 10 m high. A steel wire tied to the top of the pole is affixed at a point on the ground to keep the pole upright. If the wire makes an angle of 45° with the horizontal through the foot of the pole, find the length of the wire.
The angle of elevation of a tower from a point on the same level as the foot of the tower is 30°. On advancing 150 metres towards the foot of the tower, the angle of elevation of the tower becomes 60°. Show that the height of the tower is 129.9 metres (Use `sqrt3 = 1.732`)
An observer, 1.7 m tall, is 203–√203 m away from a tower. The angle of elevation from the of observer to the top of tower is 30°. Find the height of tower ?
The radius (in cm) of the largest right circular cone that can be cut out from a cube of edge 4.2 cm is
The angle of depression of a car parked on the road from the top of a 150 m high tower is 30º. The distance of the car from the tower (in metres) is
A statue, 2 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point, the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
A window of a house is h metres above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be α and β, respectively. Prove that the height of the other house is h(1+ tan α tan β) metres.
A pole of height 30 m is observed from a point. The angle of depression of the point is 30°. Find the distance of the point from the base of the pole.
An aeroplane when flying at a height of 3125 m from the ground passes vertically below another plane at an instant when the angles of elevation of the two planes from the same point on the ground are 30° and 60° respectively. Find the distance between the two planes at that instant.
Two poles of heights 25 m and 35 m stand vertically on the ground. The tops of two poles are connected by a wire, which is inclined to the horizontal at an angle of 30°. Find the length of the wire and the distance between the poles.
