Advertisements
Advertisements
प्रश्न
On a horizontal plane, there is a vertical tower with a flagpole on the top of the tower. At a point 9 meters away from the foot of the tower the angle of elevation of the top and bottom of the flagpole are 60° and 30° respectively. Find the height of the tower and the flagpole mounted on it.
उत्तर
Let AB be the tower of height h and AD be the flagpole on the tower. At the point 9m away from the foot of the tower, the angle of elevation of the top and bottom of the flagpole is 60° and 30°
Let AD = x, BC = 9 and ∠ACB = 30°, ∠DCB = 60°
Here we have to find the height of tower and height of the flagpole.
The corresponding diagram is as follows
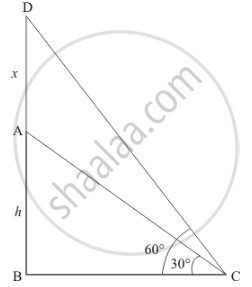
In a triangle ABC,
`=> tan C = (AB)/(BC)`
`=> tan 30^@ = h/9`
`=> 1/sqrt3 = h/9`
`=>h = 9/sqrt3`
`=> h = 3sqrt3`
Again in a triangle DBC
`=> tan C = (AD + AB)/(BC)`
`=> tan 60^@ = (h + x)/9`
`=> sqrt3 = (h + x)/9`
`=> 9sqrt3 = h + x`
`=> 9sqrt3 = 3sqrt3 + x`
`=> x = 6sqrt3`
So height of tower is `3sqrt3` meter and height of flag pole is `6sqrt3` meters
APPEARS IN
संबंधित प्रश्न
From a point P on the ground the angle of elevation of the top of a tower is 30° and that of the top of a flag staff fixed on the top of the tower, is 60°. If the length of the flag staff is 5 m, find the height of the tower.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is 30º and that of the top of the flagstaff is 45º. Find the height of the tower.
There are two temples, one on each bank of a river, just opposite to each other. One temple is 50 m high. From the top of this temple, the angles of depression of the top and the foot of the other temple are 30° and 60° respectively. Find the width of the river and the height of the other temple.
The angle of depression form the top of a tower of a point A on the ground is 30° . On moving a distance of 20 meters from the point A towards the foot of the tower to a point B, the angle of elevation of the top of the tower to from the point B is 60° . Find the height of the tower and its distance from the point A.
From the top of a hill, the angles of depression of two consecutive kilometer stones due east are found to be 45° and 30° respectivly. Find the height of the hill ?
An observer, 1.7 m tall, is 203–√203 m away from a tower. The angle of elevation from the of observer to the top of tower is 30°. Find the height of tower ?
Two buildings are facing each other on a road of width 12 metre. From the top of the first building, which is 10 metre high, the angle of elevation of the top of the second is found to be 60°. What is the height of the second building ?
The angle of elevation of a cloud from a point h metres above a lake is β. The angle of depression of its reflection in the lake is 45°. The height of location of the cloud from the lake is
A 1.5 m tall boy is standing at some distance from a 31.5 m tall building. If he walks ’d’ m towards the building the angle of elevation of the top of the building changes from 30° to 60°. Find the length d. (Take `sqrt3 = 1.73`)
At a point on level ground, the angle of elevation of a vertical tower is, found to be α such that tan α = `1/3`. After walking 100 m towards the tower, the angle of elevation β becomes such that tan β = `3/4`. Find the height of the tower.
